Arbitrary Conditional Distributions with Energy

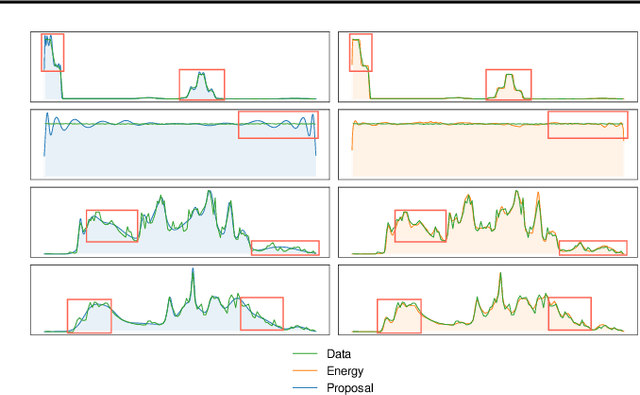
Modeling distributions of covariates, or density estimation, is a core challenge in unsupervised learning. However, the majority of work only considers the joint distribution, which has limited relevance to practical situations. A more general and useful problem is arbitrary conditional density estimation, which aims to model any possible conditional distribution over a set of covariates, reflecting the more realistic setting of inference based on prior knowledge. We propose a novel method, Arbitrary Conditioning with Energy (ACE), that can simultaneously estimate the distribution $p(\mathbf{x}_u \mid \mathbf{x}_o)$ for all possible subsets of features $\mathbf{x}_u$ and $\mathbf{x}_o$. ACE uses an energy function to specify densities, bypassing the architectural restrictions imposed by alternative methods and the biases imposed by tractable parametric distributions. We also simplify the learning problem by only learning one-dimensional conditionals, from which more complex distributions can be recovered during inference. Empirically, we show that ACE achieves state-of-the-art for arbitrary conditional and marginal likelihood estimation and for tabular data imputation.