Any Variational Autoencoder Can Do Arbitrary Conditioning

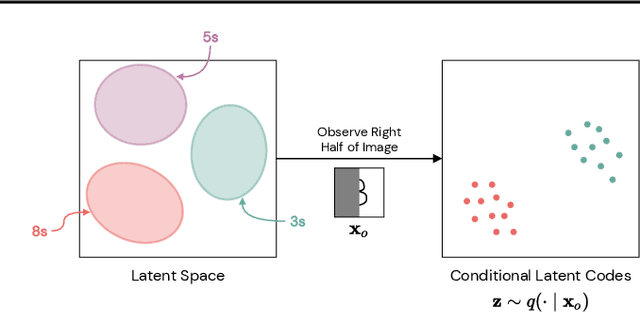
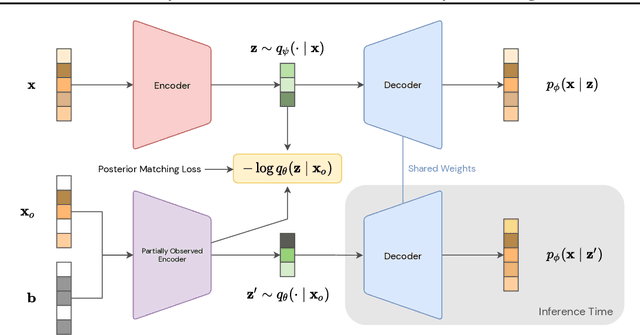
Arbitrary conditioning is an important problem in unsupervised learning, where we seek to model the conditional densities $p(\mathbf{x}_u \mid \mathbf{x}_o)$ that underly some data, for all possible non-intersecting subsets $o, u \subset \{1, \dots , d\}$. However, the vast majority of density estimation only focuses on modeling the joint distribution $p(\mathbf{x})$, in which important conditional dependencies between features are opaque. We propose a simple and general framework, coined Posterior Matching, that enables any Variational Autoencoder (VAE) to perform arbitrary conditioning, without modification to the VAE itself. Posterior Matching applies to the numerous existing VAE-based approaches to joint density estimation, thereby circumventing the specialized models required by previous approaches to arbitrary conditioning. We find that Posterior Matching achieves performance that is comparable or superior to current state-of-the-art methods for a variety of tasks.