Efficient order picking methods in robotic mobile fulfillment systems

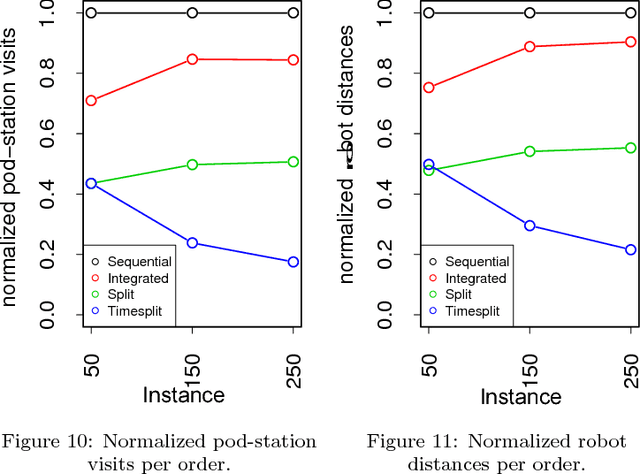
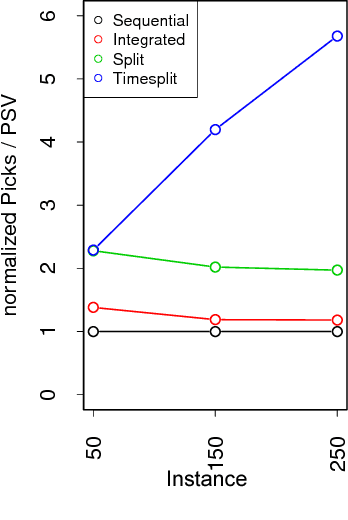
Robotic mobile fulfillment systems (RMFSs) are a new type of warehousing system, which has received more attention recently, due to increasing growth in the e-commerce sector. Instead of sending pickers to the inventory area to search for and pick the ordered items, robots carry shelves (called "pods") including ordered items from the inventory area to picking stations. In the picking stations, human pickers put ordered items into totes; then these items are transported by a conveyor to the packing stations. This type of warehousing system relieves the human pickers and improves the picking process. In this paper, we concentrate on decisions about the assignment of pods to stations and orders to stations to fulfill picking for each incoming customer's order. In previous research for an RMFS with multiple picking stations, these decisions are made sequentially. Instead, we present a new integrated model. To improve the system performance even more, we extend our model by splitting orders. This means parts of an order are allowed to be picked at different stations. To the best of the authors' knowledge, this is the first publication on split orders in an RMFS. We analyze different performance metrics, such as pile-on, pod-station visits, robot moving distance and order turn-over time. We compare the results of our models in different instances with the sequential method in our open-source simulation framework RAWSim-O.

Deterministic Pod Repositioning Problem in Robotic Mobile Fulfillment Systems

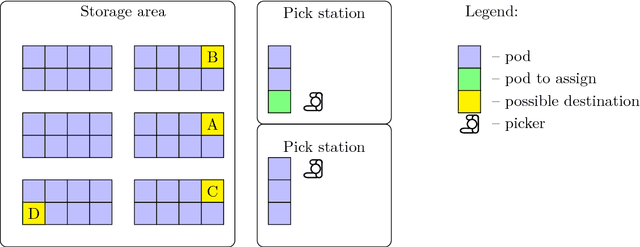
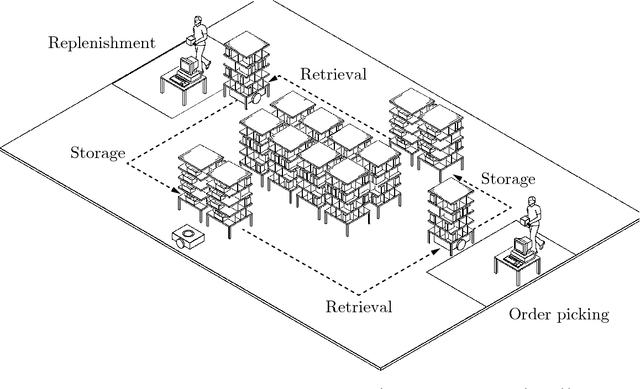
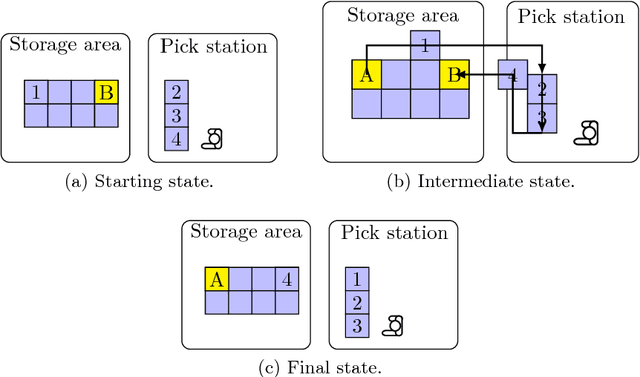
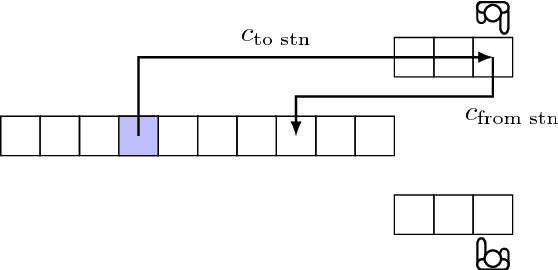
In a robotic mobile fulfillment system, robots bring shelves, called pods, with storage items from the storage area to pick stations. At every pick station there is a person -- the picker -- who takes parts from the pod and packs them into boxes according to orders. Usually there are multiple shelves at the pick station. In this case, they build a queue with the picker at its head. When the picker does not need the pod any more, a robot transports the pod back to the storage area. At that time, we need to answer a question: "Where is the optimal place in the inventory to put this pod back?". It is a tough question, because there are many uncertainties to consider before answering it. Moreover, each decision made to answer the question influences the subsequent ones. The goal of this paper is to answer the question properly. We call this problem the Pod Repositioning Problem and formulate a deterministic model. This model is tested with different algorithms, including binary integer programming, cheapest place, fixed place, random place, genetic algorithms, and a novel algorithm called tetris.