Deterministic Pod Repositioning Problem in Robotic Mobile Fulfillment Systems
Paper and Code
Oct 09, 2018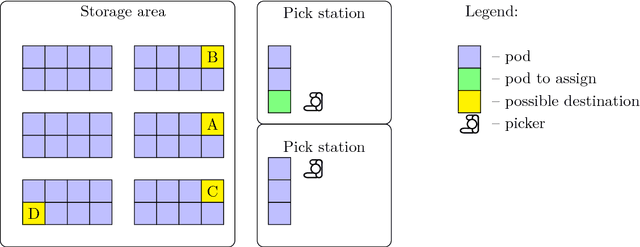
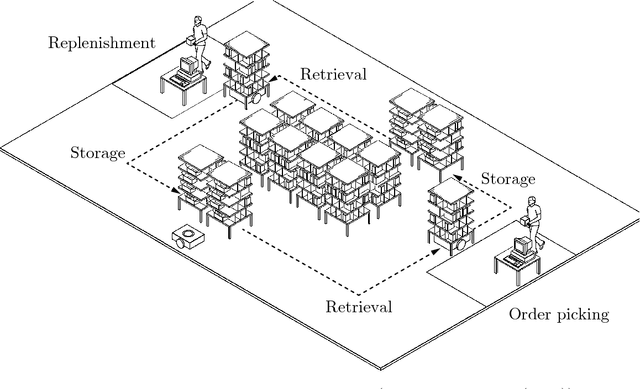
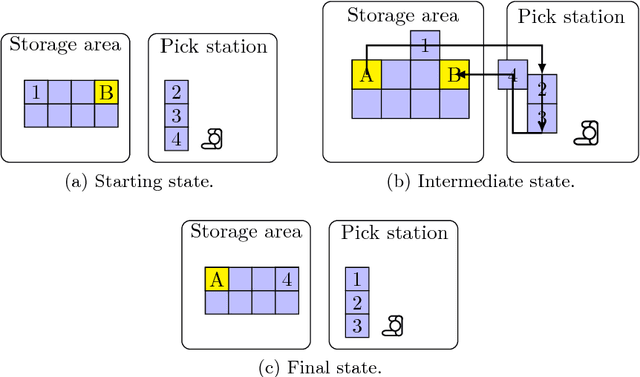
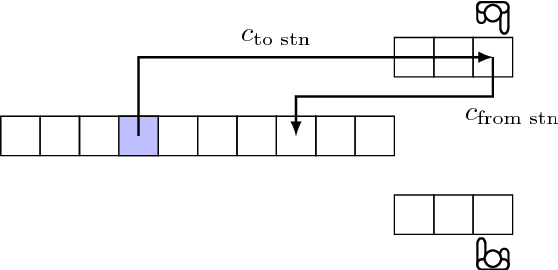
In a robotic mobile fulfillment system, robots bring shelves, called pods, with storage items from the storage area to pick stations. At every pick station there is a person -- the picker -- who takes parts from the pod and packs them into boxes according to orders. Usually there are multiple shelves at the pick station. In this case, they build a queue with the picker at its head. When the picker does not need the pod any more, a robot transports the pod back to the storage area. At that time, we need to answer a question: "Where is the optimal place in the inventory to put this pod back?". It is a tough question, because there are many uncertainties to consider before answering it. Moreover, each decision made to answer the question influences the subsequent ones. The goal of this paper is to answer the question properly. We call this problem the Pod Repositioning Problem and formulate a deterministic model. This model is tested with different algorithms, including binary integer programming, cheapest place, fixed place, random place, genetic algorithms, and a novel algorithm called tetris.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge