Self-Distillation Improves DNA Sequence Inference

Self-supervised pretraining (SSP) has been recognized as a method to enhance prediction accuracy in various downstream tasks. However, its efficacy for DNA sequences remains somewhat constrained. This limitation stems primarily from the fact that most existing SSP approaches in genomics focus on masked language modeling of individual sequences, neglecting the crucial aspect of encoding statistics across multiple sequences. To overcome this challenge, we introduce an innovative deep neural network model, which incorporates collaborative learning between a `student' and a `teacher' subnetwork. In this model, the student subnetwork employs masked learning on nucleotides and progressively adapts its parameters to the teacher subnetwork through an exponential moving average approach. Concurrently, both subnetworks engage in contrastive learning, deriving insights from two augmented representations of the input sequences. This self-distillation process enables our model to effectively assimilate both contextual information from individual sequences and distributional data across the sequence population. We validated our approach with preliminary pretraining using the human reference genome, followed by applying it to 20 downstream inference tasks. The empirical results from these experiments demonstrate that our novel method significantly boosts inference performance across the majority of these tasks. Our code is available at https://github.com/wiedersehne/FinDNA.

ChordMixer: A Scalable Neural Attention Model for Sequences with Different Lengths

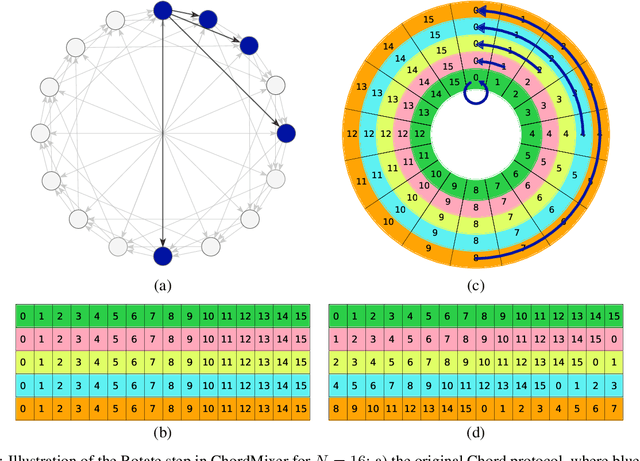
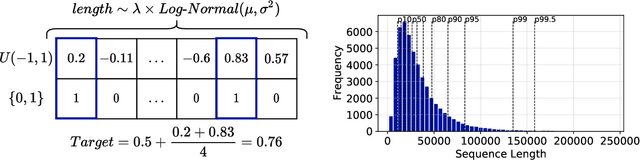
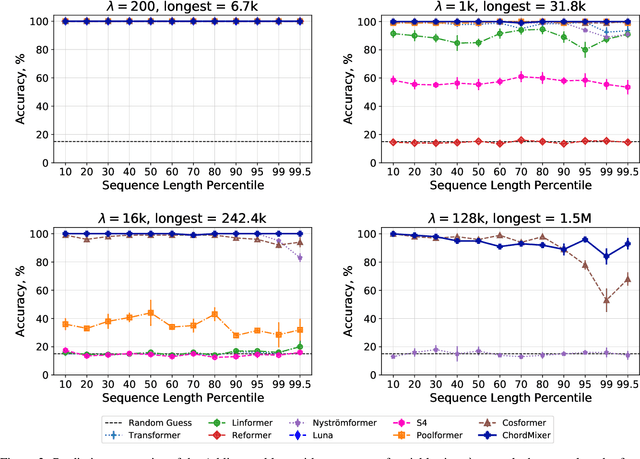
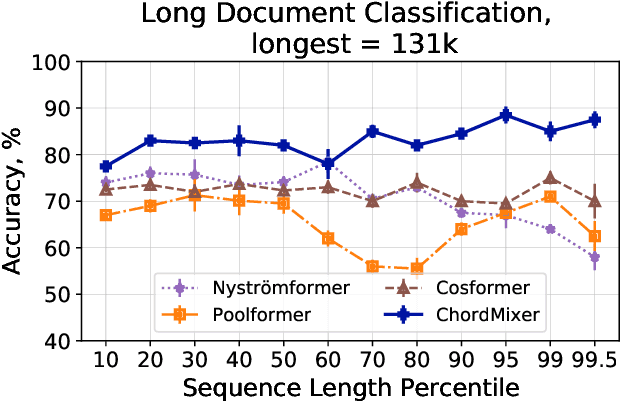
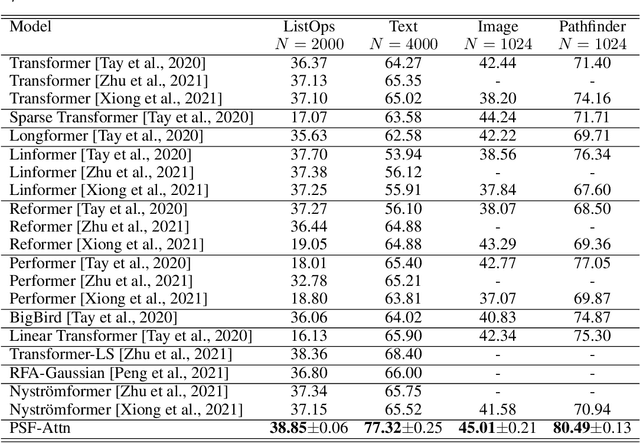
Sequential data naturally have different lengths in many domains, with some very long sequences. As an important modeling tool, neural attention should capture long-range interaction in such sequences. However, most existing neural attention models admit only short sequences, or they have to employ chunking or padding to enforce a constant input length. Here we propose a simple neural network building block called ChordMixer which can model the attention for long sequences with variable lengths. Each ChordMixer block consists of a position-wise rotation layer without learnable parameters and an element-wise MLP layer. Repeatedly applying such blocks forms an effective network backbone that mixes the input signals towards the learning targets. We have tested ChordMixer on the synthetic adding problem, long document classification, and DNA sequence-based taxonomy classification. The experiment results show that our method substantially outperforms other neural attention models.

Paramixer: Parameterizing Mixing Links in Sparse Factors Works Better than Dot-Product Self-Attention

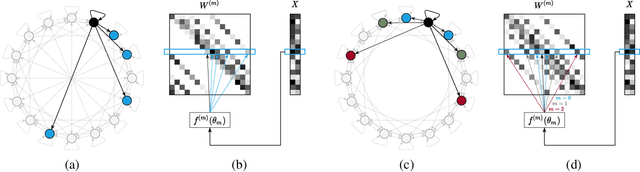
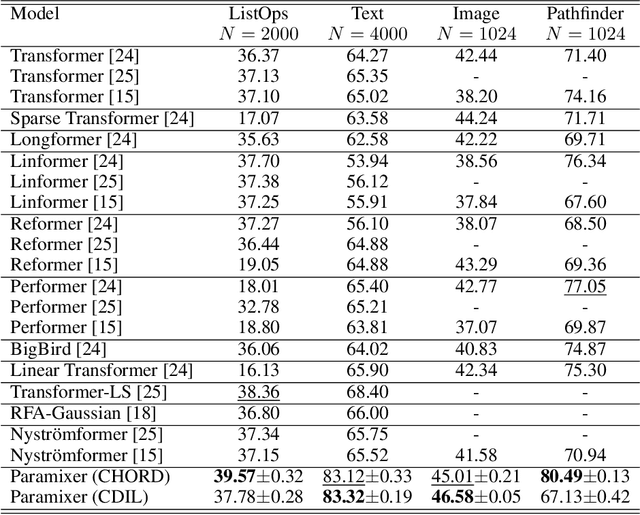
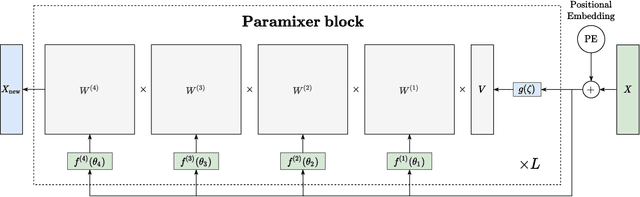
Self-Attention is a widely used building block in neural modeling to mix long-range data elements. Most self-attention neural networks employ pairwise dot-products to specify the attention coefficients. However, these methods require $O(N^2)$ computing cost for sequence length $N$. Even though some approximation methods have been introduced to relieve the quadratic cost, the performance of the dot-product approach is still bottlenecked by the low-rank constraint in the attention matrix factorization. In this paper, we propose a novel scalable and effective mixing building block called Paramixer. Our method factorizes the interaction matrix into several sparse matrices, where we parameterize the non-zero entries by MLPs with the data elements as input. The overall computing cost of the new building block is as low as $O(N \log N)$. Moreover, all factorizing matrices in Paramixer are full-rank, so it does not suffer from the low-rank bottleneck. We have tested the new method on both synthetic and various real-world long sequential data sets and compared it with several state-of-the-art attention networks. The experimental results show that Paramixer has better performance in most learning tasks.

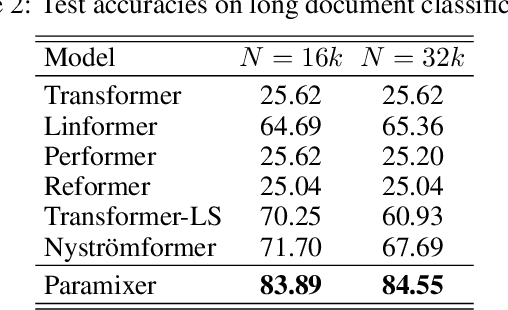
Classification of Long Sequential Data using Circular Dilated Convolutional Neural Networks

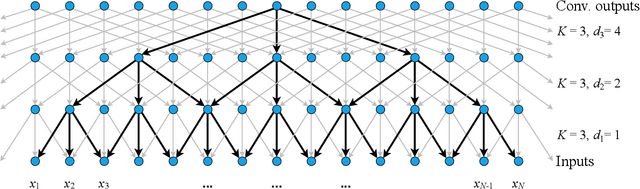
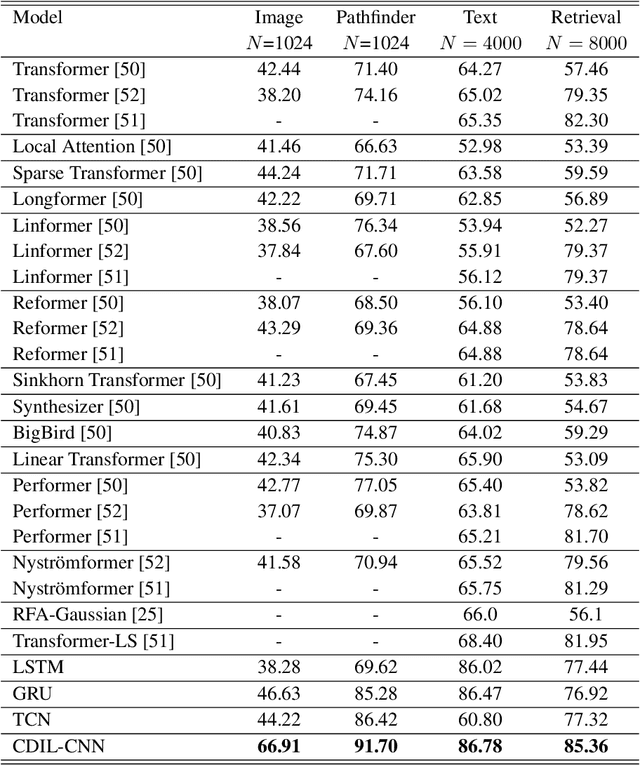
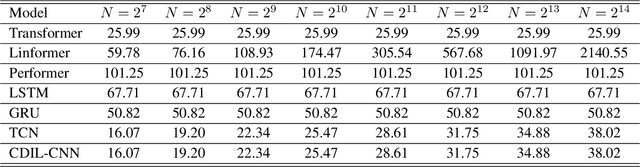
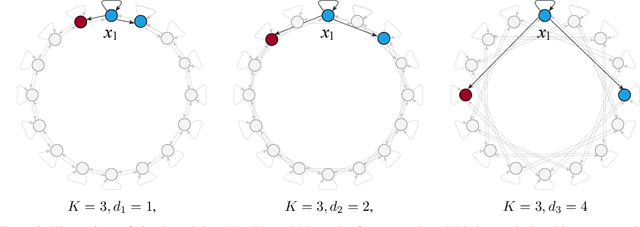
Classification of long sequential data is an important Machine Learning task and appears in many application scenarios. Recurrent Neural Networks, Transformers, and Convolutional Neural Networks are three major techniques for learning from sequential data. Among these methods, Temporal Convolutional Networks (TCNs) which are scalable to very long sequences have achieved remarkable progress in time series regression. However, the performance of TCNs for sequence classification is not satisfactory because they use a skewed connection protocol and output classes at the last position. Such asymmetry restricts their performance for classification which depends on the whole sequence. In this work, we propose a symmetric multi-scale architecture called Circular Dilated Convolutional Neural Network (CDIL-CNN), where every position has an equal chance to receive information from other positions at the previous layers. Our model gives classification logits in all positions, and we can apply a simple ensemble learning to achieve a better decision. We have tested CDIL-CNN on various long sequential datasets. The experimental results show that our method has superior performance over many state-of-the-art approaches.

Sparse Factorization of Large Square Matrices

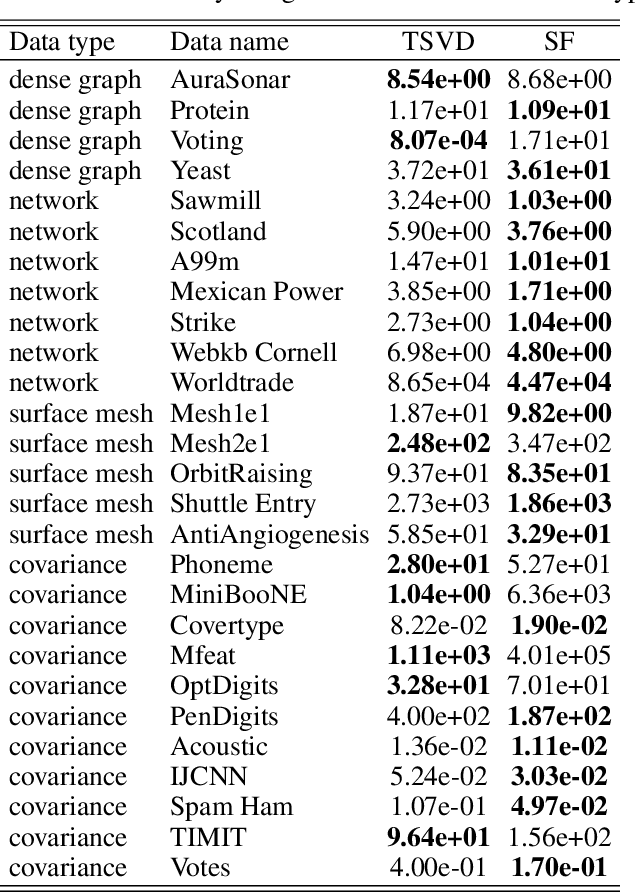
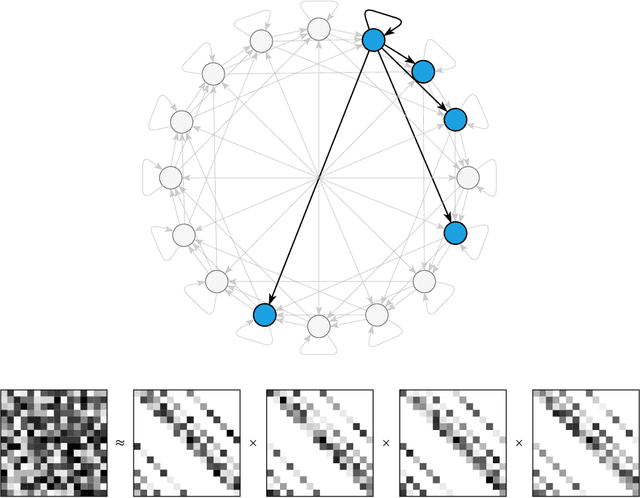
Square matrices appear in many machine learning problems and models. Optimization over a large square matrix is expensive in memory and in time. Therefore an economic approximation is needed. Conventional approximation approaches factorize the square matrix into a number matrices of much lower ranks. However, the low-rank constraint is a performance bottleneck if the approximated matrix is intrinsically high-rank or close to full rank. In this paper, we propose to approximate a large square matrix with a product of sparse full-rank matrices. In the approximation, our method needs only $N(\log N)^2$ non-zero numbers for an $N\times N$ full matrix. We present both non-parametric and parametric ways to find the factorization. In the former, we learn the factorizing matrices directly, and in the latter, we train neural networks to map input data to the non-zero matrix entries. The sparse factorization method is tested for a variety of synthetic and real-world square matrices. The experimental results demonstrate that our method gives a better approximation when the approximated matrix is sparse and high-rank. Based on this finding, we use our parametric method as a scalable attention architecture that performs strongly in learning tasks for long sequential data and defeats Transformer and its several variants.