Paramixer: Parameterizing Mixing Links in Sparse Factors Works Better than Dot-Product Self-Attention
Paper and Code
Apr 22, 2022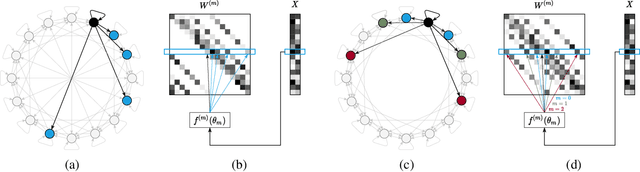
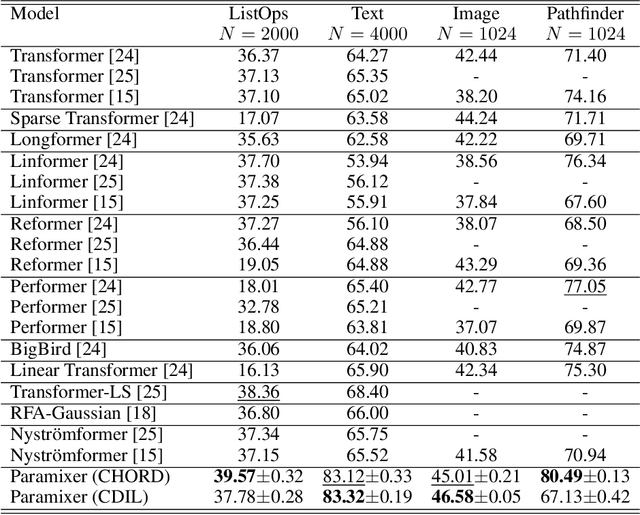
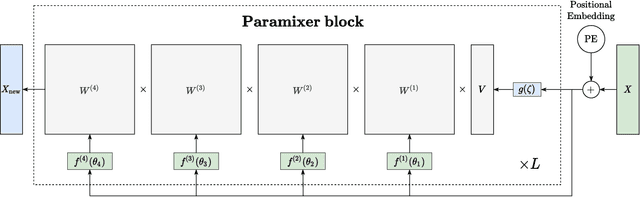
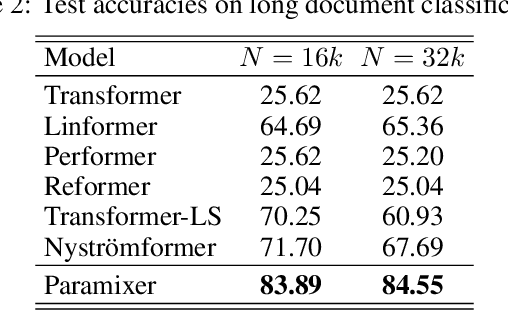
Self-Attention is a widely used building block in neural modeling to mix long-range data elements. Most self-attention neural networks employ pairwise dot-products to specify the attention coefficients. However, these methods require $O(N^2)$ computing cost for sequence length $N$. Even though some approximation methods have been introduced to relieve the quadratic cost, the performance of the dot-product approach is still bottlenecked by the low-rank constraint in the attention matrix factorization. In this paper, we propose a novel scalable and effective mixing building block called Paramixer. Our method factorizes the interaction matrix into several sparse matrices, where we parameterize the non-zero entries by MLPs with the data elements as input. The overall computing cost of the new building block is as low as $O(N \log N)$. Moreover, all factorizing matrices in Paramixer are full-rank, so it does not suffer from the low-rank bottleneck. We have tested the new method on both synthetic and various real-world long sequential data sets and compared it with several state-of-the-art attention networks. The experimental results show that Paramixer has better performance in most learning tasks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge