Accurately Predicting Probabilities of Safety-Critical Rare Events for Intelligent Systems

Intelligent systems are increasingly integral to our daily lives, yet rare safety-critical events present significant latent threats to their practical deployment. Addressing this challenge hinges on accurately predicting the probability of safety-critical events occurring within a given time step from the current state, a metric we define as 'criticality'. The complexity of predicting criticality arises from the extreme data imbalance caused by rare events in high dimensional variables associated with the rare events, a challenge we refer to as the curse of rarity. Existing methods tend to be either overly conservative or prone to overlooking safety-critical events, thus struggling to achieve both high precision and recall rates, which severely limits their applicability. This study endeavors to develop a criticality prediction model that excels in both precision and recall rates for evaluating the criticality of safety-critical autonomous systems. We propose a multi-stage learning framework designed to progressively densify the dataset, mitigating the curse of rarity across stages. To validate our approach, we evaluate it in two cases: lunar lander and bipedal walker scenarios. The results demonstrate that our method surpasses traditional approaches, providing a more accurate and dependable assessment of criticality in intelligent systems.

Adaptive Testing Environment Generation for Connected and Automated Vehicles with Dense Reinforcement Learning

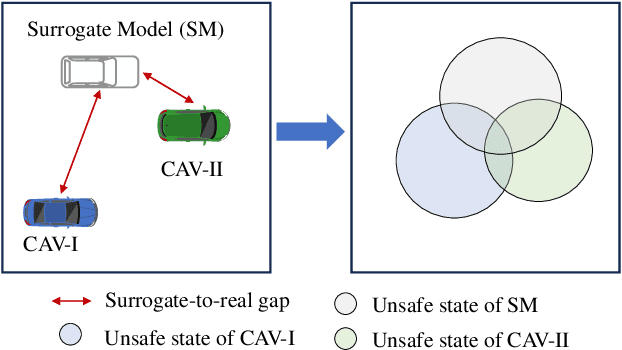
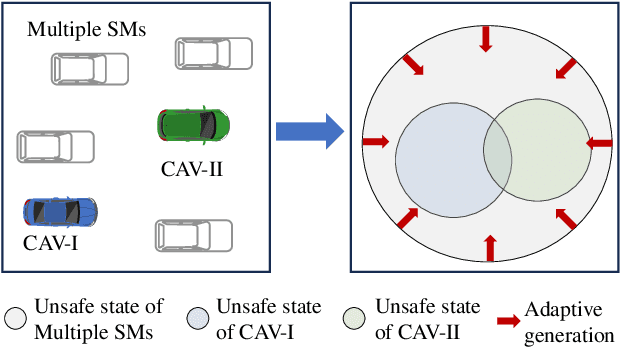
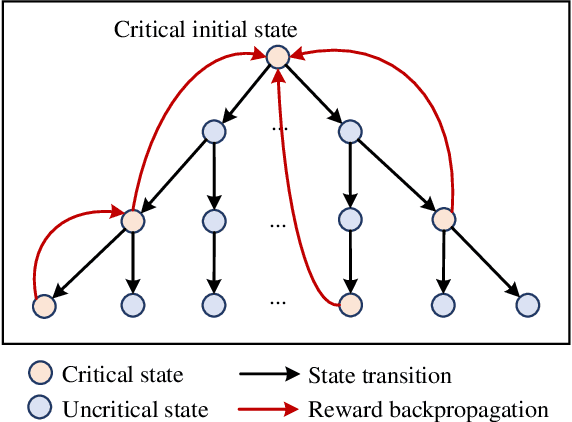
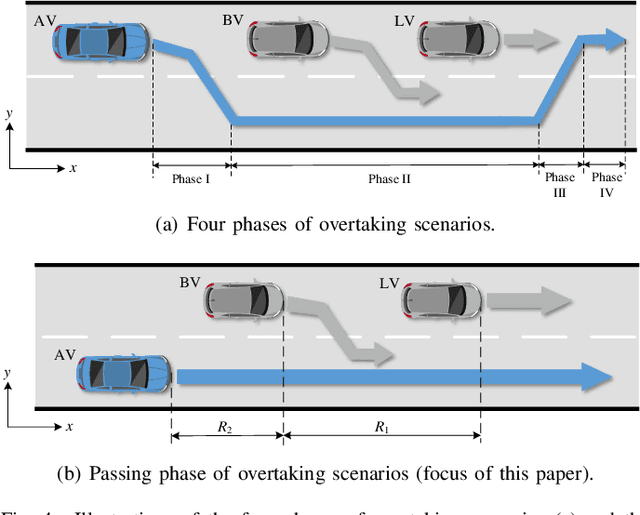
The assessment of safety performance plays a pivotal role in the development and deployment of connected and automated vehicles (CAVs). A common approach involves designing testing scenarios based on prior knowledge of CAVs (e.g., surrogate models), conducting tests in these scenarios, and subsequently evaluating CAVs' safety performances. However, substantial differences between CAVs and the prior knowledge can significantly diminish the evaluation efficiency. In response to this issue, existing studies predominantly concentrate on the adaptive design of testing scenarios during the CAV testing process. Yet, these methods have limitations in their applicability to high-dimensional scenarios. To overcome this challenge, we develop an adaptive testing environment that bolsters evaluation robustness by incorporating multiple surrogate models and optimizing the combination coefficients of these surrogate models to enhance evaluation efficiency. We formulate the optimization problem as a regression task utilizing quadratic programming. To efficiently obtain the regression target via reinforcement learning, we propose the dense reinforcement learning method and devise a new adaptive policy with high sample efficiency. Essentially, our approach centers on learning the values of critical scenes displaying substantial surrogate-to-real gaps. The effectiveness of our method is validated in high-dimensional overtaking scenarios, demonstrating that our approach achieves notable evaluation efficiency.