Adaptive Selective Sampling for Online Prediction with Experts

We consider online prediction of a binary sequence with expert advice. For this setting, we devise label-efficient forecasting algorithms, which use a selective sampling scheme that enables collecting much fewer labels than standard procedures, while still retaining optimal worst-case regret guarantees. These algorithms are based on exponentially weighted forecasters, suitable for settings with and without a perfect expert. For a scenario where one expert is strictly better than the others in expectation, we show that the label complexity of the label-efficient forecaster scales roughly as the square root of the number of rounds. Finally, we present numerical experiments empirically showing that the normalized regret of the label-efficient forecaster can asymptotically match known minimax rates for pool-based active learning, suggesting it can optimally adapt to benign settings.

A Statistical Model for Dynamic Networks with Neural Variational Inference

In this paper we propose a statistical model for dynamically evolving networks, together with a variational inference approach. Our model, which we call Dynamic Latent Attribute Interaction Model (DLAIM), encodes edge dependencies across different time snapshots. It represents nodes via latent attributes and uses attribute interaction matrices to model the presence of edges. Both are allowed to evolve with time, thus allowing us to capture the dynamics of the network. We develop a neural network based variational inference procedure that provides a suitable way to learn the model parameters. The main strengths of DLAIM are: (i) it is flexible as it does not impose strict assumptions on network evolution unlike existing approaches, (ii) it applies to both directed as well as undirected networks, and more importantly, (iii) learned node attributes and interaction matrices may be interpretable and therefore provide insights on the mechanisms behind network evolution. Experiments done on real world networks for the task of link forecasting demonstrate the superior performance of our model as compared to existing approaches.

Restricted Boltzmann Stochastic Block Model: A Generative Model for Networks with Attributes

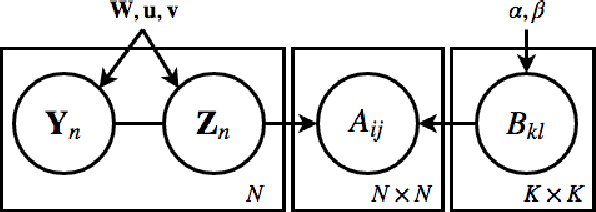
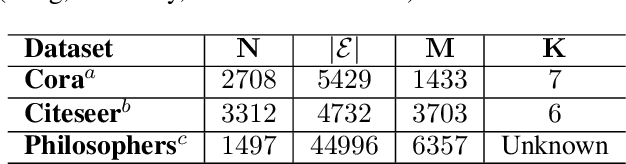
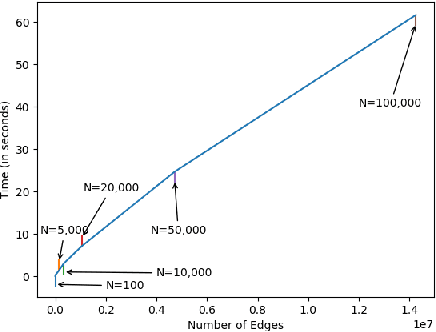
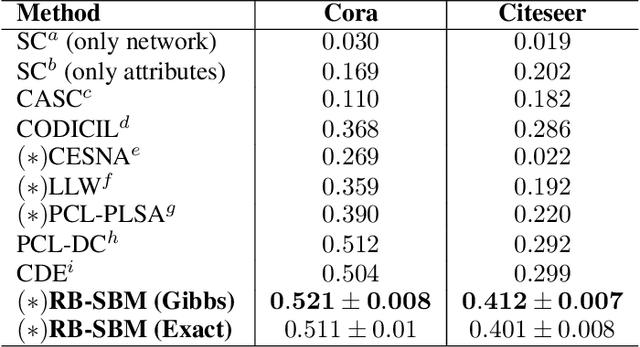
In most practical contexts network indexed data consists not only of a description about the presence/absence of links, but also attributes and information about the nodes and/or links. Building on success of Stochastic Block Models (SBM) we propose a simple yet powerful generalization of SBM for networks with node attributes. In a standard SBM the rows of latent community membership matrix are sampled from a multinomial. In RB-SBM, our proposed model, these rows are sampled from a Restricted Boltzmann Machine (RBM) that models a joint distribution over observed attributes and latent community membership. This model has the advantage of being simple while combining connectivity and attribute information, and it has very few tuning parameters. Furthermore, we show that inference can be done efficiently in linear time and it can be naturally extended to accommodate, for instance, overlapping communities. We demonstrate the performance of our model on multiple synthetic and real world networks with node attributes where we obtain state-of-the-art results on the task of community detection.