Neural Descriptors: Self-Supervised Learning of Robust Local Surface Descriptors Using Polynomial Patches

Classical shape descriptors such as Heat Kernel Signature (HKS), Wave Kernel Signature (WKS), and Signature of Histograms of OrienTations (SHOT), while widely used in shape analysis, exhibit sensitivity to mesh connectivity, sampling patterns, and topological noise. While differential geometry offers a promising alternative through its theory of differential invariants, which are theoretically guaranteed to be robust shape descriptors, the computation of these invariants on discrete meshes often leads to unstable numerical approximations, limiting their practical utility. We present a self-supervised learning approach for extracting geometric features from 3D surfaces. Our method combines synthetic data generation with a neural architecture designed to learn sampling-invariant features. By integrating our features into existing shape correspondence frameworks, we demonstrate improved performance on standard benchmarks including FAUST, SCAPE, TOPKIDS, and SHREC'16, showing particular robustness to topological noise and partial shapes.

Pathways on the Image Manifold: Image Editing via Video Generation

Recent advances in image editing, driven by image diffusion models, have shown remarkable progress. However, significant challenges remain, as these models often struggle to follow complex edit instructions accurately and frequently compromise fidelity by altering key elements of the original image. Simultaneously, video generation has made remarkable strides, with models that effectively function as consistent and continuous world simulators. In this paper, we propose merging these two fields by utilizing image-to-video models for image editing. We reformulate image editing as a temporal process, using pretrained video models to create smooth transitions from the original image to the desired edit. This approach traverses the image manifold continuously, ensuring consistent edits while preserving the original image's key aspects. Our approach achieves state-of-the-art results on text-based image editing, demonstrating significant improvements in both edit accuracy and image preservation.

Learning Differential Invariants of Planar Curves

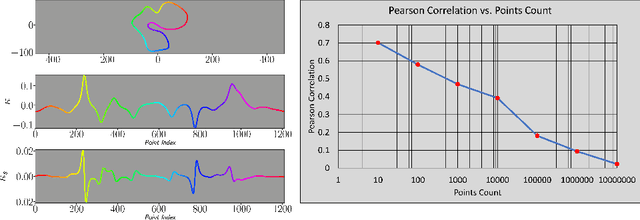
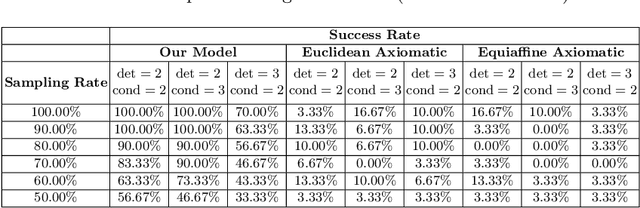
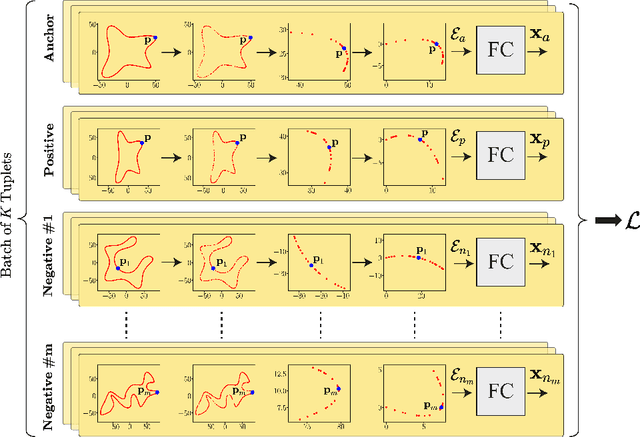
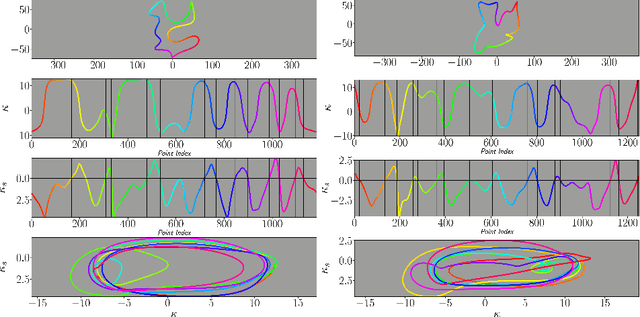
We propose a learning paradigm for the numerical approximation of differential invariants of planar curves. Deep neural-networks' (DNNs) universal approximation properties are utilized to estimate geometric measures. The proposed framework is shown to be a preferable alternative to axiomatic constructions. Specifically, we show that DNNs can learn to overcome instabilities and sampling artifacts and produce consistent signatures for curves subject to a given group of transformations in the plane. We compare the proposed schemes to alternative state-of-the-art axiomatic constructions of differential invariants. We evaluate our models qualitatively and quantitatively and propose a benchmark dataset to evaluate approximation models of differential invariants of planar curves.

Deep Signatures -- Learning Invariants of Planar Curves

We propose a learning paradigm for numerical approximation of differential invariants of planar curves. Deep neural-networks' (DNNs) universal approximation properties are utilized to estimate geometric measures. The proposed framework is shown to be a preferable alternative to axiomatic constructions. Specifically, we show that DNNs can learn to overcome instabilities and sampling artifacts and produce numerically-stable signatures for curves subject to a given group of transformations in the plane. We compare the proposed schemes to alternative state-of-the-art axiomatic constructions of group invariant arc-lengths and curvatures.