Fractional-Order Federated Learning

Federated learning (FL) allows remote clients to train a global model collaboratively while protecting client privacy. Despite its privacy-preserving benefits, FL has significant drawbacks, including slow convergence, high communication cost, and non-independent-and-identically-distributed (non-IID) data. In this work, we present a novel FedAvg variation called Fractional-Order Federated Averaging (FOFedAvg), which incorporates Fractional-Order Stochastic Gradient Descent (FOSGD) to capture long-range relationships and deeper historical information. By introducing memory-aware fractional-order updates, FOFedAvg improves communication efficiency and accelerates convergence while mitigating instability caused by heterogeneous, non-IID client data. We compare FOFedAvg against a broad set of established federated optimization algorithms on benchmark datasets including MNIST, FEMNIST, CIFAR-10, CIFAR-100, EMNIST, the Cleveland heart disease dataset, Sent140, PneumoniaMNIST, and Edge-IIoTset. Across a range of non-IID partitioning schemes, FOFedAvg is competitive with, and often outperforms, these baselines in terms of test performance and convergence speed. On the theoretical side, we prove that FOFedAvg converges to a stationary point under standard smoothness and bounded-variance assumptions for fractional order $0<α\le 1$. Together, these results show that fractional-order, memory-aware updates can substantially improve the robustness and effectiveness of federated learning, offering a practical path toward distributed training on heterogeneous data.

Fractional Order Federated Learning for Battery Electric Vehicle Energy Consumption Modeling

Federated learning on connected electric vehicles (BEVs) faces severe instability due to intermittent connectivity, time-varying client participation, and pronounced client-to-client variation induced by diverse operating conditions. Conventional FedAvg and many advanced methods can suffer from excessive drift and degraded convergence under these realistic constraints. This work introduces Fractional-Order Roughness-Informed Federated Averaging (FO-RI-FedAvg), a lightweight and modular extension of FedAvg that improves stability through two complementary client-side mechanisms: (i) adaptive roughness-informed proximal regularization, which dynamically tunes the pull toward the global model based on local loss-landscape roughness, and (ii) non-integer-order local optimization, which incorporates short-term memory to smooth conflicting update directions. The approach preserves standard FedAvg server aggregation, adds only element-wise operations with amortizable overhead, and allows independent toggling of each component. Experiments on two real-world BEV energy prediction datasets, VED and its extended version eVED, show that FO-RI-FedAvg achieves improved accuracy and more stable convergence compared to strong federated baselines, particularly under reduced client participation.

When Gradient Clipping Becomes a Control Mechanism for Differential Privacy in Deep Learning

Privacy-preserving training on sensitive data commonly relies on differentially private stochastic optimization with gradient clipping and Gaussian noise. The clipping threshold is a critical control knob: if set too small, systematic over-clipping induces optimization bias; if too large, injected noise dominates updates and degrades accuracy. Existing adaptive clipping methods often depend on per-example gradient norm statistics, adding computational overhead and introducing sensitivity to datasets and architectures. We propose a control-driven clipping strategy that adapts the threshold using a lightweight, weight-only spectral diagnostic computed from model parameters. At periodic probe steps, the method analyzes a designated weight matrix via spectral decomposition and estimates a heavy-tailed spectral indicator associated with training stability. This indicator is smoothed over time and fed into a bounded feedback controller that updates the clipping threshold multiplicatively in the log domain. Because the controller uses only parameters produced during privacy-preserving training, the resulting threshold updates are post-processing and do not increase privacy loss beyond that of the underlying DP optimizer under standard composition accounting.

Roughness-Informed Federated Learning

Federated Learning (FL) enables collaborative model training across distributed clients while preserving data privacy, yet faces challenges in non-independent and identically distributed (non-IID) settings due to client drift, which impairs convergence. We propose RI-FedAvg, a novel FL algorithm that mitigates client drift by incorporating a Roughness Index (RI)-based regularization term into the local objective, adaptively penalizing updates based on the fluctuations of local loss landscapes. This paper introduces RI-FedAvg, leveraging the RI to quantify the roughness of high-dimensional loss functions, ensuring robust optimization in heterogeneous settings. We provide a rigorous convergence analysis for non-convex objectives, establishing that RI-FedAvg converges to a stationary point under standard assumptions. Extensive experiments on MNIST, CIFAR-10, and CIFAR-100 demonstrate that RI-FedAvg outperforms state-of-the-art baselines, including FedAvg, FedProx, FedDyn, SCAFFOLD, and DP-FedAvg, achieving higher accuracy and faster convergence in non-IID scenarios. Our results highlight RI-FedAvg's potential to enhance the robustness and efficiency of federated learning in practical, heterogeneous environments.

Statistical Roughness-Informed Machine Unlearning

Machine unlearning aims to remove the influence of a designated forget set from a trained model while preserving utility on the retained data. In modern deep networks, approximate unlearning frequently fails under large or adversarial deletions due to pronounced layer-wise heterogeneity: some layers exhibit stable, well-regularized representations while others are brittle, undertrained, or overfit, so naive update allocation can trigger catastrophic forgetting or unstable dynamics. We propose Statistical-Roughness Adaptive Gradient Unlearning (SRAGU), a mechanism-first unlearning algorithm that reallocates unlearning updates using layer-wise statistical roughness operationalized via heavy-tailed spectral diagnostics of layer weight matrices. Starting from an Adaptive Gradient Unlearning (AGU) sensitivity signal computed on the forget set, SRAGU estimates a WeightWatcher-style heavy-tailed exponent for each layer, maps it to a bounded spectral stability weight, and uses this stability signal to spectrally reweight the AGU sensitivities before applying the same minibatch update form. This concentrates unlearning motion in spectrally stable layers while damping updates in unstable or overfit layers, improving stability under hard deletions. We evaluate unlearning via behavioral alignment to a gold retrained reference model trained from scratch on the retained data, using empirical prediction-divergence and KL-to-gold proxies on a forget-focused query set; we additionally report membership inference auditing as a complementary leakage signal, treating forget-set points as should-be-forgotten members during evaluation.

More Optimal Fractional-Order Stochastic Gradient Descent for Non-Convex Optimization Problems

Fractional-order stochastic gradient descent (FOSGD) leverages fractional exponents to capture long-memory effects in optimization. However, its utility is often limited by the difficulty of tuning and stabilizing these exponents. We propose 2SED Fractional-Order Stochastic Gradient Descent (2SEDFOSGD), which integrates the Two-Scale Effective Dimension (2SED) algorithm with FOSGD to adapt the fractional exponent in a data-driven manner. By tracking model sensitivity and effective dimensionality, 2SEDFOSGD dynamically modulates the exponent to mitigate oscillations and hasten convergence. Theoretically, for onoconvex optimization problems, this approach preserves the advantages of fractional memory without the sluggish or unstable behavior observed in na\"ive fractional SGD. Empirical evaluations in Gaussian and $\alpha$-stable noise scenarios using an autoregressive (AR) model highlight faster convergence and more robust parameter estimates compared to baseline methods, underscoring the potential of dimension-aware fractional techniques for advanced modeling and estimation tasks.

Effective Dimension Aware Fractional-Order Stochastic Gradient Descent for Convex Optimization Problems

Fractional-order stochastic gradient descent (FOSGD) leverages a fractional exponent to capture long-memory effects in optimization, yet its practical impact is often constrained by the difficulty of tuning and stabilizing this exponent. In this work, we introduce 2SED Fractional-Order Stochastic Gradient Descent (2SEDFOSGD), a novel method that synergistically combines the Two-Scale Effective Dimension (2SED) algorithm with FOSGD to automatically calibrate the fractional exponent in a data-driven manner. By continuously gauging model sensitivity and effective dimensionality, 2SED dynamically adjusts the exponent to curb erratic oscillations and enhance convergence rates. Theoretically, we demonstrate how this dimension-aware adaptation retains the benefits of fractional memory while averting the sluggish or unstable behaviors frequently observed in naive fractional SGD. Empirical evaluations across multiple benchmarks confirm that our 2SED-driven fractional exponent approach not only converges faster but also achieves more robust final performance, suggesting broad applicability for fractional-order methodologies in large-scale machine learning and related domains.

Symmetric Rank-One Quasi-Newton Methods for Deep Learning Using Cubic Regularization

Stochastic gradient descent and other first-order variants, such as Adam and AdaGrad, are commonly used in the field of deep learning due to their computational efficiency and low-storage memory requirements. However, these methods do not exploit curvature information. Consequently, iterates can converge to saddle points or poor local minima. On the other hand, Quasi-Newton methods compute Hessian approximations which exploit this information with a comparable computational budget. Quasi-Newton methods re-use previously computed iterates and gradients to compute a low-rank structured update. The most widely used quasi-Newton update is the L-BFGS, which guarantees a positive semi-definite Hessian approximation, making it suitable in a line search setting. However, the loss functions in DNNs are non-convex, where the Hessian is potentially non-positive definite. In this paper, we propose using a limited-memory symmetric rank-one quasi-Newton approach which allows for indefinite Hessian approximations, enabling directions of negative curvature to be exploited. Furthermore, we use a modified adaptive regularized cubics approach, which generates a sequence of cubic subproblems that have closed-form solutions with suitable regularization choices. We investigate the performance of our proposed method on autoencoders and feed-forward neural network models and compare our approach to state-of-the-art first-order adaptive stochastic methods as well as other quasi-Newton methods.x

Sequential anomaly detection in the presence of noise and limited feedback

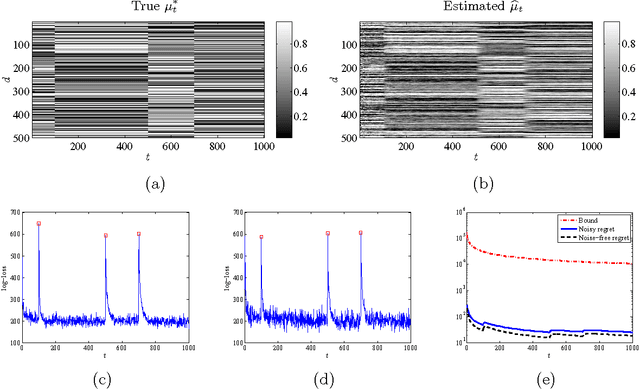
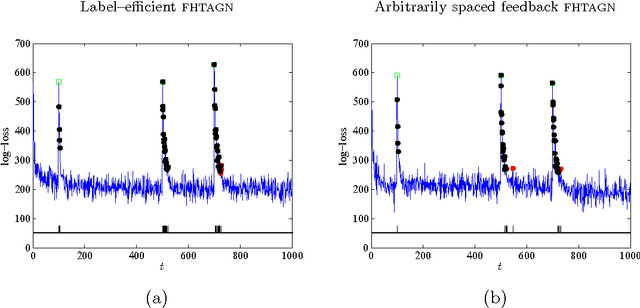
This paper describes a methodology for detecting anomalies from sequentially observed and potentially noisy data. The proposed approach consists of two main elements: (1) {\em filtering}, or assigning a belief or likelihood to each successive measurement based upon our ability to predict it from previous noisy observations, and (2) {\em hedging}, or flagging potential anomalies by comparing the current belief against a time-varying and data-adaptive threshold. The threshold is adjusted based on the available feedback from an end user. Our algorithms, which combine universal prediction with recent work on online convex programming, do not require computing posterior distributions given all current observations and involve simple primal-dual parameter updates. At the heart of the proposed approach lie exponential-family models which can be used in a wide variety of contexts and applications, and which yield methods that achieve sublinear per-round regret against both static and slowly varying product distributions with marginals drawn from the same exponential family. Moreover, the regret against static distributions coincides with the minimax value of the corresponding online strongly convex game. We also prove bounds on the number of mistakes made during the hedging step relative to the best offline choice of the threshold with access to all estimated beliefs and feedback signals. We validate the theory on synthetic data drawn from a time-varying distribution over binary vectors of high dimensionality, as well as on the Enron email dataset.