Adam through a Second-Order Lens

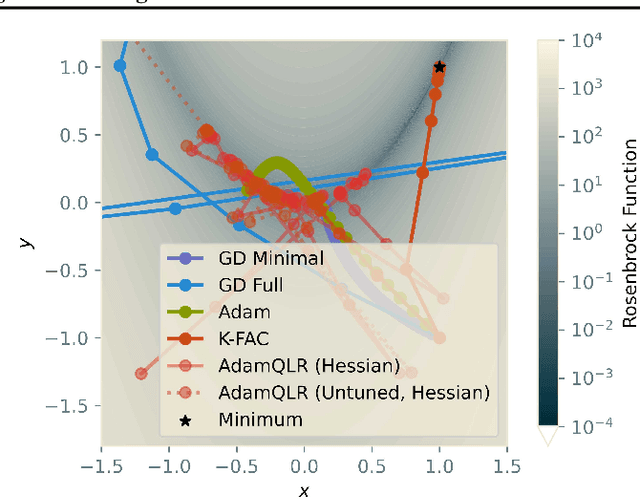
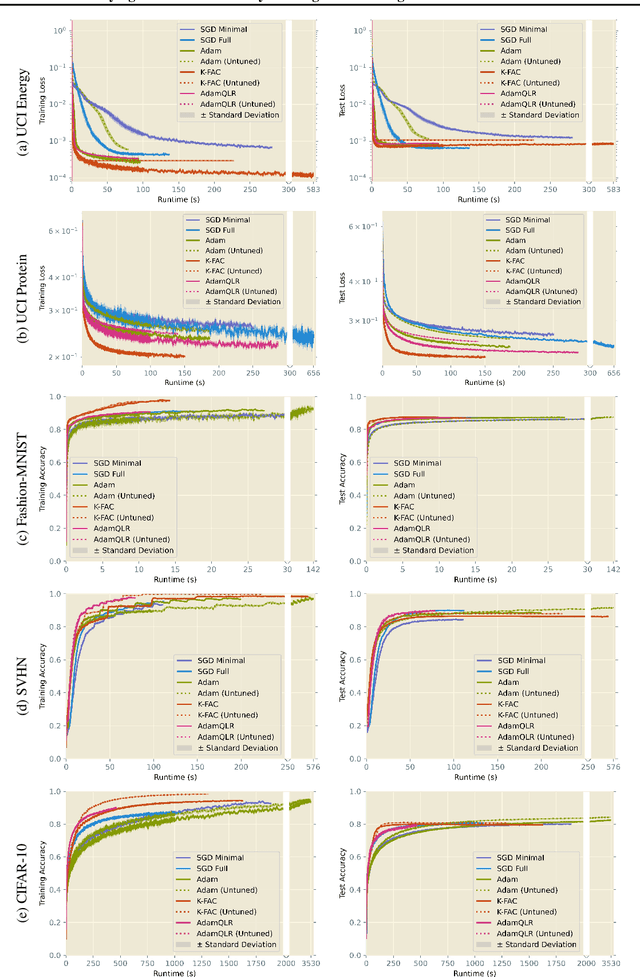
Research into optimisation for deep learning is characterised by a tension between the computational efficiency of first-order, gradient-based methods (such as SGD and Adam) and the theoretical efficiency of second-order, curvature-based methods (such as quasi-Newton methods and K-FAC). We seek to combine the benefits of both approaches into a single computationally-efficient algorithm. Noting that second-order methods often depend on stabilising heuristics (such as Levenberg-Marquardt damping), we propose AdamQLR: an optimiser combining damping and learning rate selection techniques from K-FAC (Martens and Grosse, 2015) with the update directions proposed by Adam, inspired by considering Adam through a second-order lens. We evaluate AdamQLR on a range of regression and classification tasks at various scales, achieving competitive generalisation performance vs runtime.

Series of Hessian-Vector Products for Tractable Saddle-Free Newton Optimisation of Neural Networks

Despite their popularity in the field of continuous optimisation, second-order quasi-Newton methods are challenging to apply in machine learning, as the Hessian matrix is intractably large. This computational burden is exacerbated by the need to address non-convexity, for instance by modifying the Hessian's eigenvalues as in Saddle-Free Newton methods. We propose an optimisation algorithm which addresses both of these concerns - to our knowledge, the first efficiently-scalable optimisation algorithm to asymptotically use the exact (eigenvalue-modified) inverse Hessian. Our method frames the problem as a series which principally square-roots and inverts the squared Hessian, then uses it to precondition a gradient vector, all without explicitly computing or eigendecomposing the Hessian. A truncation of this infinite series provides a new optimisation algorithm which is scalable and comparable to other first- and second-order optimisation methods in both runtime and optimisation performance. We demonstrate this in a variety of settings, including a ResNet-18 trained on CIFAR-10.

Scalable One-Pass Optimisation of High-Dimensional Weight-Update Hyperparameters by Implicit Differentiation

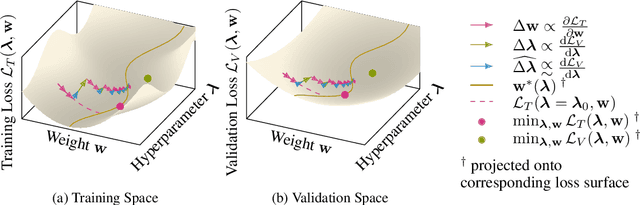
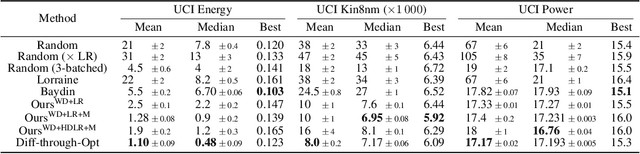
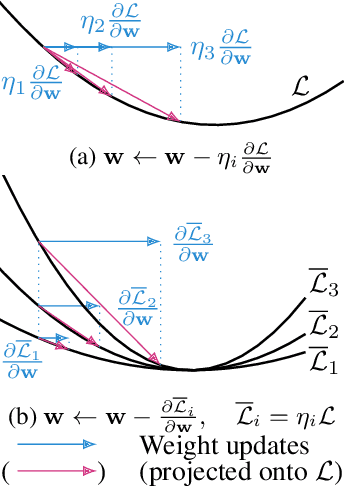
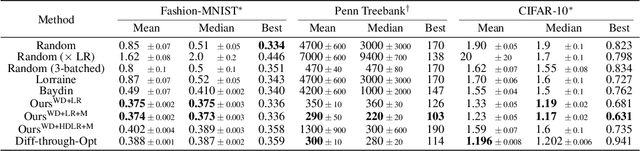
Machine learning training methods depend plentifully and intricately on hyperparameters, motivating automated strategies for their optimisation. Many existing algorithms restart training for each new hyperparameter choice, at considerable computational cost. Some hypergradient-based one-pass methods exist, but these either cannot be applied to arbitrary optimiser hyperparameters (such as learning rates and momenta) or take several times longer to train than their base models. We extend these existing methods to develop an approximate hypergradient-based hyperparameter optimiser which is applicable to any continuous hyperparameter appearing in a differentiable model weight update, yet requires only one training episode, with no restarts. We also provide a motivating argument for convergence to the true hypergradient, and perform tractable gradient-based optimisation of independent learning rates for each model parameter. Our method performs competitively from varied random hyperparameter initialisations on several UCI datasets and Fashion-MNIST (using a one-layer MLP), Penn Treebank (using an LSTM) and CIFAR-10 (using a ResNet-18), in time only 2-3x greater than vanilla training.