Scalable One-Pass Optimisation of High-Dimensional Weight-Update Hyperparameters by Implicit Differentiation
Paper and Code
Oct 20, 2021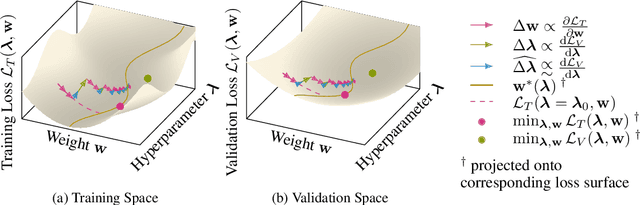
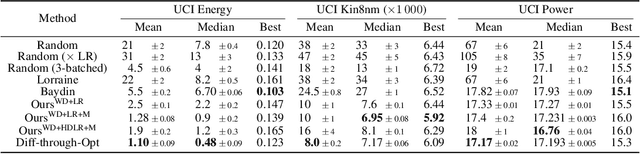
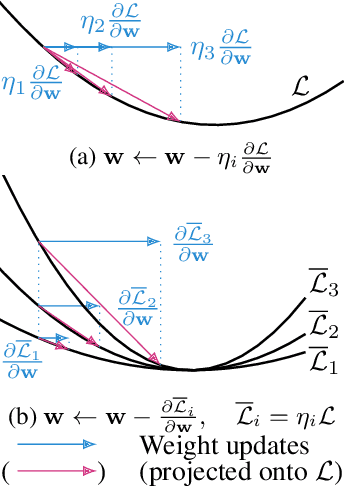
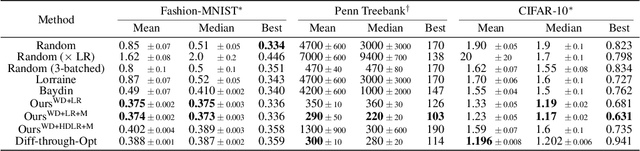
Machine learning training methods depend plentifully and intricately on hyperparameters, motivating automated strategies for their optimisation. Many existing algorithms restart training for each new hyperparameter choice, at considerable computational cost. Some hypergradient-based one-pass methods exist, but these either cannot be applied to arbitrary optimiser hyperparameters (such as learning rates and momenta) or take several times longer to train than their base models. We extend these existing methods to develop an approximate hypergradient-based hyperparameter optimiser which is applicable to any continuous hyperparameter appearing in a differentiable model weight update, yet requires only one training episode, with no restarts. We also provide a motivating argument for convergence to the true hypergradient, and perform tractable gradient-based optimisation of independent learning rates for each model parameter. Our method performs competitively from varied random hyperparameter initialisations on several UCI datasets and Fashion-MNIST (using a one-layer MLP), Penn Treebank (using an LSTM) and CIFAR-10 (using a ResNet-18), in time only 2-3x greater than vanilla training.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge