Biasless Language Models Learn Unnaturally: How LLMs Fail to Distinguish the Possible from the Impossible

Are large language models (LLMs) sensitive to the distinction between humanly possible languages and humanly impossible languages? This question is taken by many to bear on whether LLMs and humans share the same innate learning biases. Previous work has attempted to answer it in the positive by comparing LLM learning curves on existing language datasets and on "impossible" datasets derived from them via various perturbation functions. Using the same methodology, we examine this claim on a wider set of languages and impossible perturbations. We find that in most cases, GPT-2 learns each language and its impossible counterpart equally easily, in contrast to previous claims. We also apply a more lenient condition by testing whether GPT-2 provides any kind of separation between the whole set of natural languages and the whole set of impossible languages. By considering cross-linguistic variance in various metrics computed on the perplexity curves, we show that GPT-2 provides no systematic separation between the possible and the impossible. Taken together, these perspectives show that LLMs do not share the human innate biases that shape linguistic typology.

Large Language Models as Proxies for Theories of Human Linguistic Cognition

We consider the possible role of current large language models (LLMs) in the study of human linguistic cognition. We focus on the use of such models as proxies for theories of cognition that are relatively linguistically-neutral in their representations and learning but differ from current LLMs in key ways. We illustrate this potential use of LLMs as proxies for theories of cognition in the context of two kinds of questions: (a) whether the target theory accounts for the acquisition of a given pattern from a given corpus; and (b) whether the target theory makes a given typologically-attested pattern easier to acquire than another, typologically-unattested pattern. For each of the two questions we show, building on recent literature, how current LLMs can potentially be of help, but we note that at present this help is quite limited.

Bridging the Empirical-Theoretical Gap in Neural Network Formal Language Learning Using Minimum Description Length

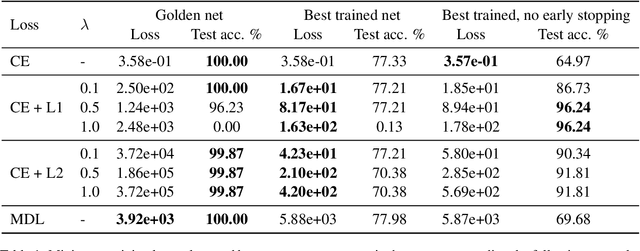
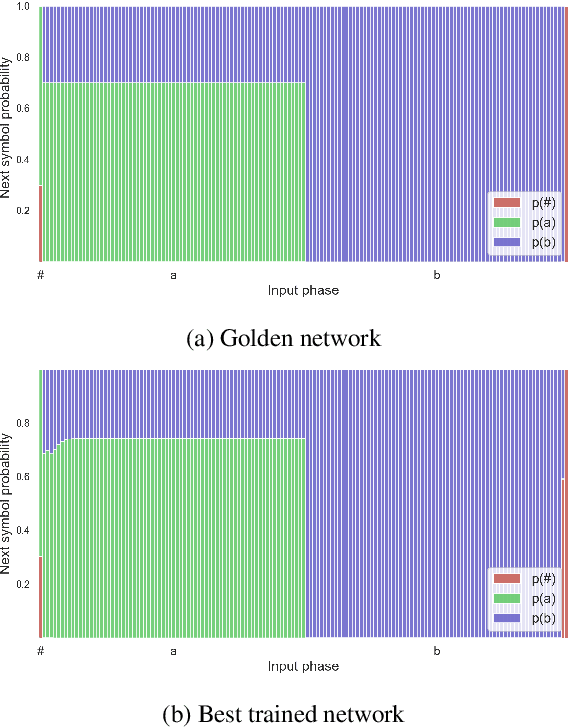
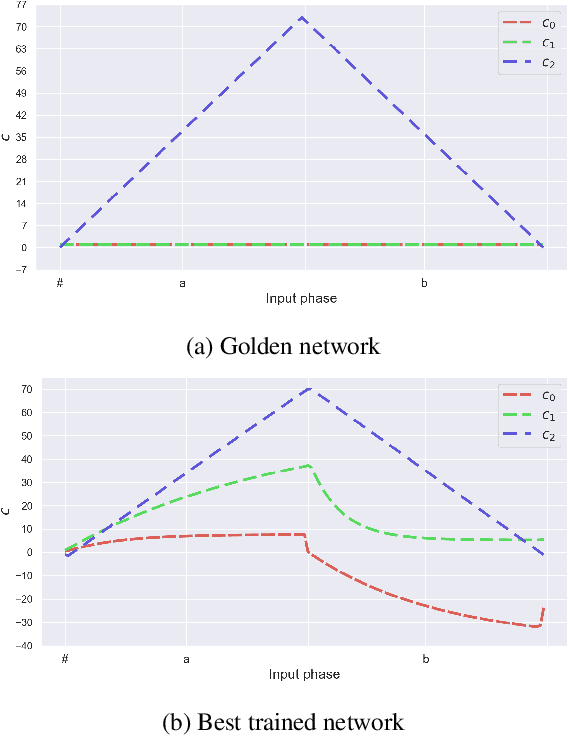
Neural networks offer good approximation to many tasks but consistently fail to reach perfect generalization, even when theoretical work shows that such perfect solutions can be expressed by certain architectures. Using the task of formal language learning, we focus on one simple formal language and show that the theoretically correct solution is in fact not an optimum of commonly used objectives -- even with regularization techniques that according to common wisdom should lead to simple weights and good generalization (L1, L2) or other meta-heuristics (early-stopping, dropout). However, replacing standard targets with the Minimum Description Length objective (MDL) results in the correct solution being an optimum.

Minimum Description Length Hopfield Networks

Associative memory architectures are designed for memorization but also offer, through their retrieval method, a form of generalization to unseen inputs: stored memories can be seen as prototypes from this point of view. Focusing on Modern Hopfield Networks (MHN), we show that a large memorization capacity undermines the generalization opportunity. We offer a solution to better optimize this tradeoff. It relies on Minimum Description Length (MDL) to determine during training which memories to store, as well as how many of them.

Benchmarking Neural Network Generalization for Grammar Induction

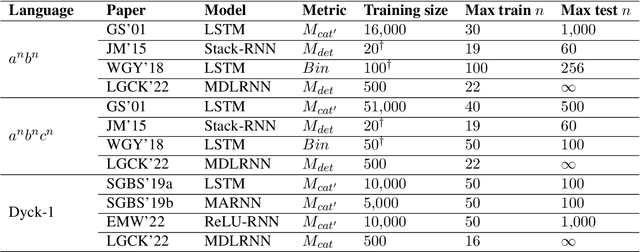
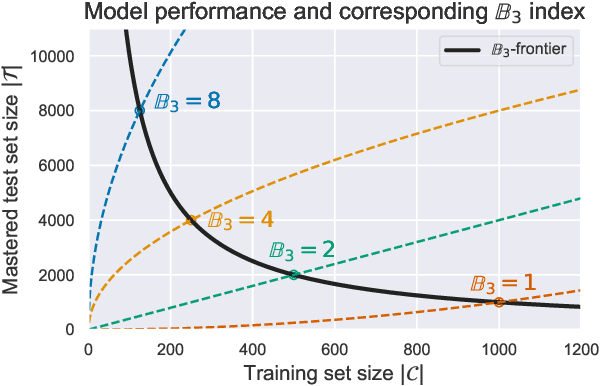
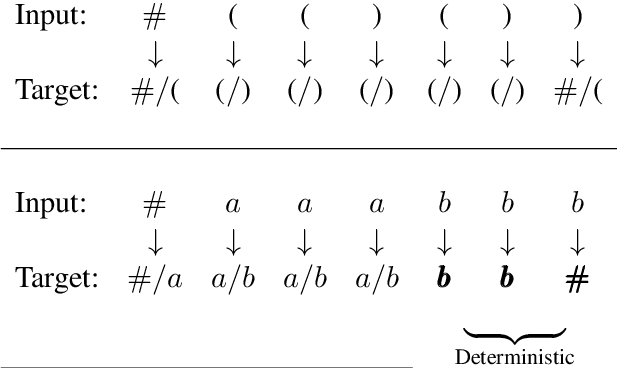
How well do neural networks generalize? Even for grammar induction tasks, where the target generalization is fully known, previous works have left the question open, testing very limited ranges beyond the training set and using different success criteria. We provide a measure of neural network generalization based on fully specified formal languages. Given a model and a formal grammar, the method assigns a generalization score representing how well a model generalizes to unseen samples in inverse relation to the amount of data it was trained on. The benchmark includes languages such as $a^nb^n$, $a^nb^nc^n$, $a^nb^mc^{n+m}$, and Dyck-1 and 2. We evaluate selected architectures using the benchmark and find that networks trained with a Minimum Description Length objective (MDL) generalize better and using less data than networks trained using standard loss functions. The benchmark is available at https://github.com/taucompling/bliss.

Minimum Description Length Recurrent Neural Networks

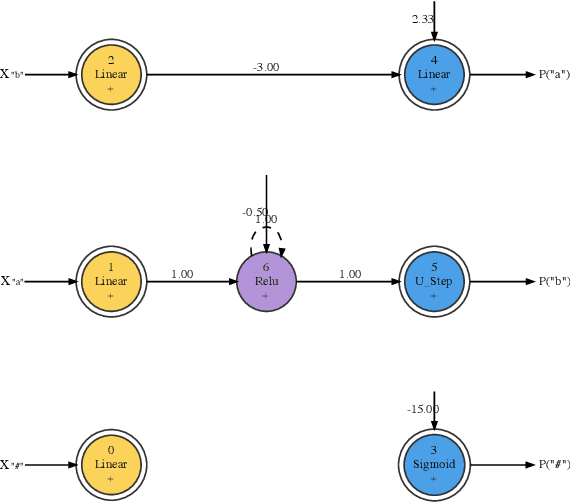
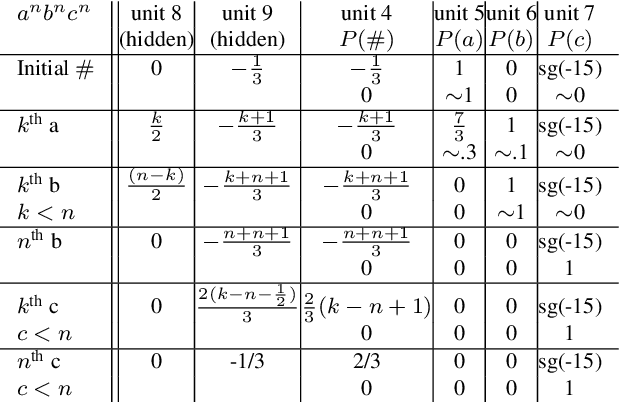
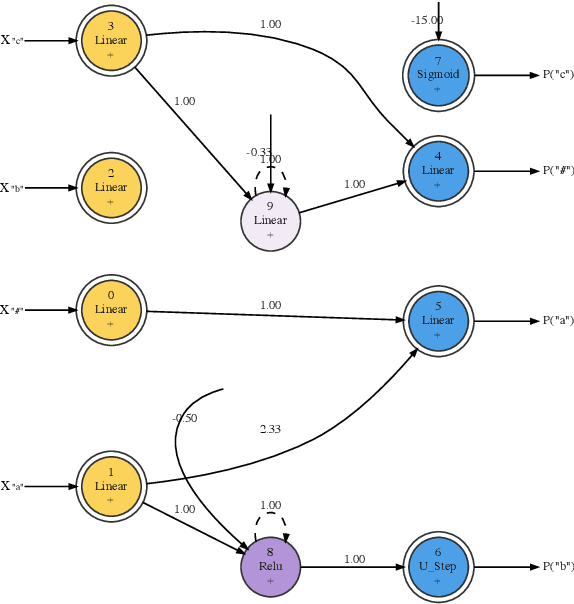
We train neural networks to optimize a Minimum Description Length score, i.e., to balance between the complexity of the network and its accuracy at a task. We show that networks trained with this objective function master tasks involving memory challenges such as counting, including cases that go beyond context-free languages. These learners master grammars for, e.g., $a^nb^n$, $a^nb^nc^n$, $a^nb^{2n}$, and $a^nb^mc^{n+m}$, and they perform addition. They do so with 100% accuracy, sometimes also with 100% confidence. The networks are also small and their inner workings are transparent. We thus provide formal proofs that their perfect accuracy holds not only on a given test set, but for any input sequence.