Minimum Description Length Recurrent Neural Networks

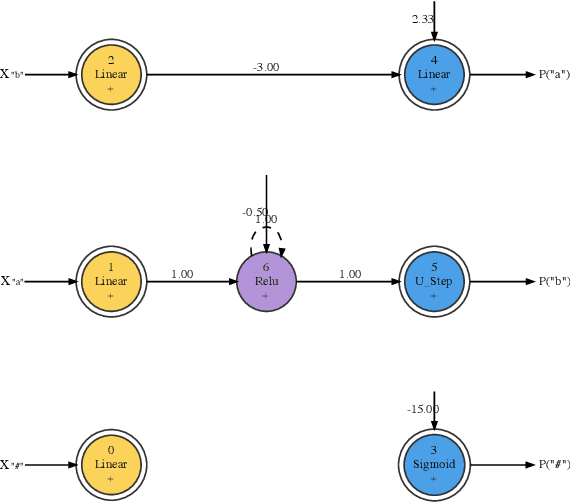
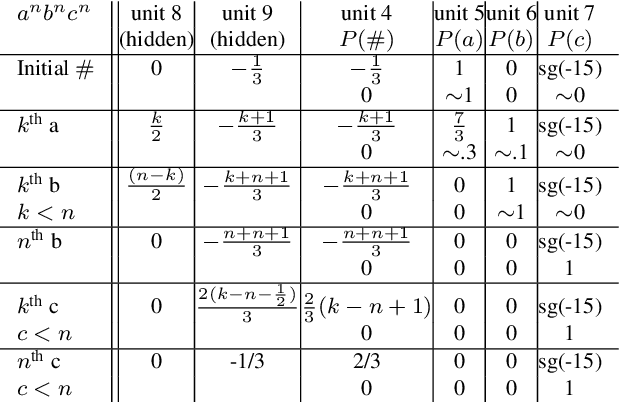
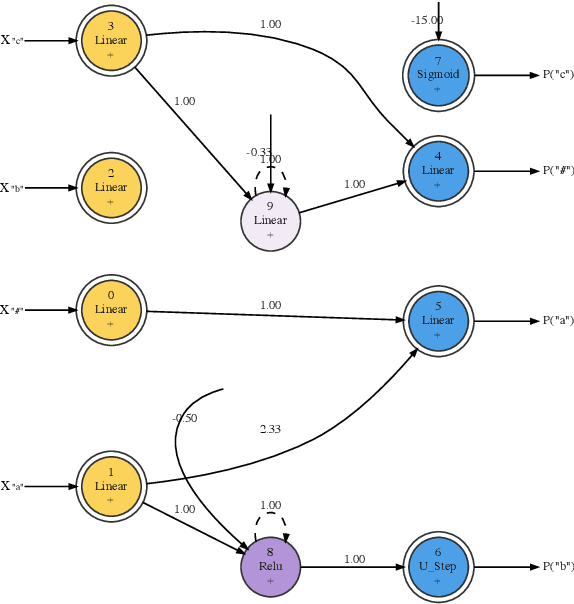
We train neural networks to optimize a Minimum Description Length score, i.e., to balance between the complexity of the network and its accuracy at a task. We show that networks trained with this objective function master tasks involving memory challenges such as counting, including cases that go beyond context-free languages. These learners master grammars for, e.g., $a^nb^n$, $a^nb^nc^n$, $a^nb^{2n}$, and $a^nb^mc^{n+m}$, and they perform addition. They do so with 100% accuracy, sometimes also with 100% confidence. The networks are also small and their inner workings are transparent. We thus provide formal proofs that their perfect accuracy holds not only on a given test set, but for any input sequence.