Bridging the Empirical-Theoretical Gap in Neural Network Formal Language Learning Using Minimum Description Length
Paper and Code
Feb 15, 2024
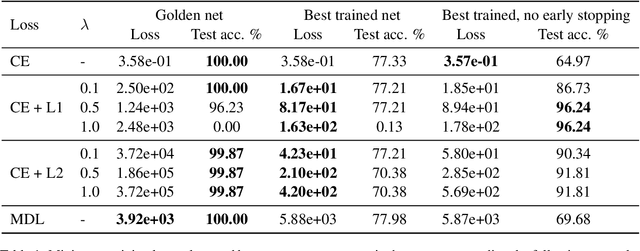
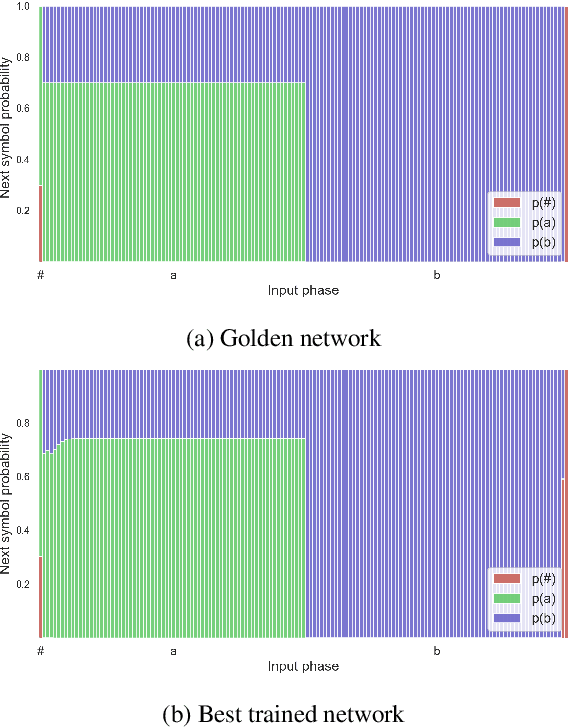
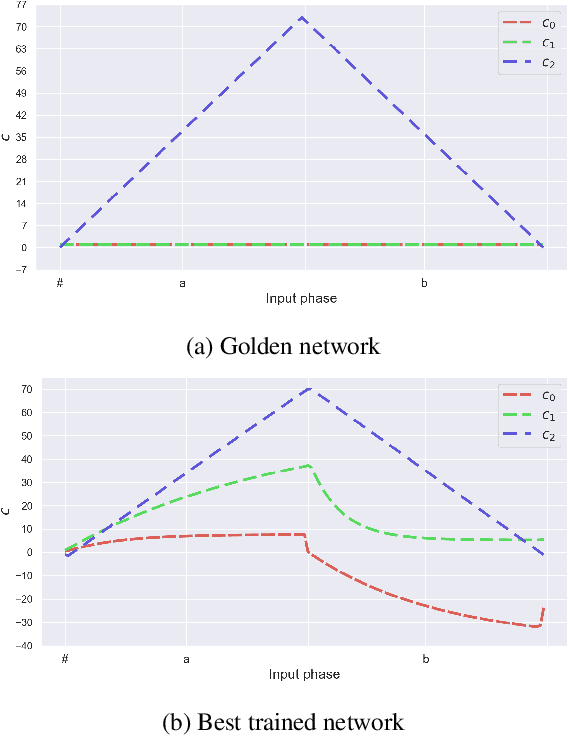
Neural networks offer good approximation to many tasks but consistently fail to reach perfect generalization, even when theoretical work shows that such perfect solutions can be expressed by certain architectures. Using the task of formal language learning, we focus on one simple formal language and show that the theoretically correct solution is in fact not an optimum of commonly used objectives -- even with regularization techniques that according to common wisdom should lead to simple weights and good generalization (L1, L2) or other meta-heuristics (early-stopping, dropout). However, replacing standard targets with the Minimum Description Length objective (MDL) results in the correct solution being an optimum.
* 9 pages, 5 figures, 3 appendix pages
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge