Ronald Fick
A Hierarchical Spatial Transformer for Massive Point Samples in Continuous Space
Nov 08, 2023Abstract:Transformers are widely used deep learning architectures. Existing transformers are mostly designed for sequences (texts or time series), images or videos, and graphs. This paper proposes a novel transformer model for massive (up to a million) point samples in continuous space. Such data are ubiquitous in environment sciences (e.g., sensor observations), numerical simulations (e.g., particle-laden flow, astrophysics), and location-based services (e.g., POIs and trajectories). However, designing a transformer for massive spatial points is non-trivial due to several challenges, including implicit long-range and multi-scale dependency on irregular points in continuous space, a non-uniform point distribution, the potential high computational costs of calculating all-pair attention across massive points, and the risks of over-confident predictions due to varying point density. To address these challenges, we propose a new hierarchical spatial transformer model, which includes multi-resolution representation learning within a quad-tree hierarchy and efficient spatial attention via coarse approximation. We also design an uncertainty quantification branch to estimate prediction confidence related to input feature noise and point sparsity. We provide a theoretical analysis of computational time complexity and memory costs. Extensive experiments on both real-world and synthetic datasets show that our method outperforms multiple baselines in prediction accuracy and our model can scale up to one million points on one NVIDIA A100 GPU. The code is available at \url{https://github.com/spatialdatasciencegroup/HST}.
Robust Semi-Supervised Classification using GANs with Self-Organizing Maps
Oct 19, 2021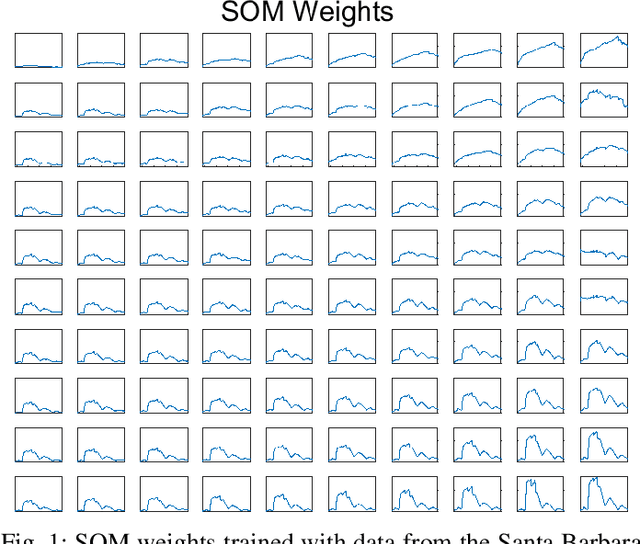
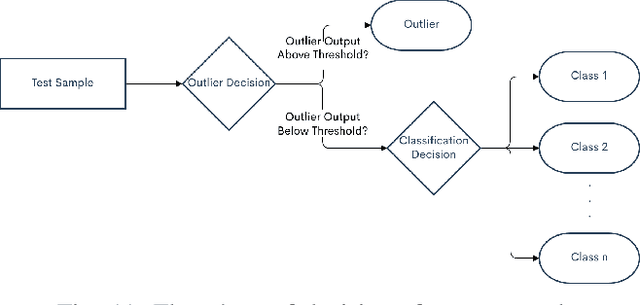
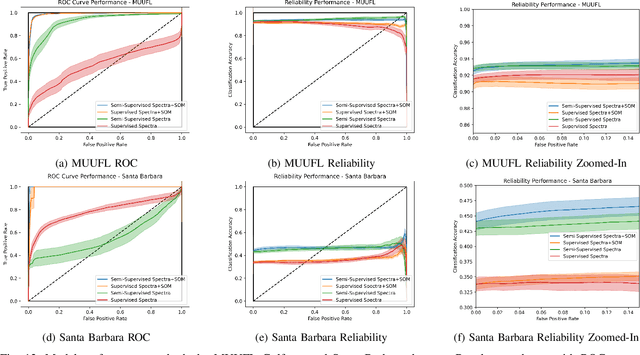
Abstract:Generative adversarial networks (GANs) have shown tremendous promise in learning to generate data and effective at aiding semi-supervised classification. However, to this point, semi-supervised GAN methods make the assumption that the unlabeled data set contains only samples of the joint distribution of the classes of interest, referred to as inliers. Consequently, when presented with a sample from other distributions, referred to as outliers, GANs perform poorly at determining that it is not qualified to make a decision on the sample. The problem of discriminating outliers from inliers while maintaining classification accuracy is referred to here as the DOIC problem. In this work, we describe an architecture that combines self-organizing maps (SOMs) with SS-GANS with the goal of mitigating the DOIC problem and experimental results indicating that the architecture achieves the goal. Multiple experiments were conducted on hyperspectral image data sets. The SS-GANS performed slightly better than supervised GANS on classification problems with and without the SOM. Incorporating the SOMs into the SS-GANs and the supervised GANS led to substantially mitigation of the DOIC problem when compared to SS-GANS and GANs without the SOMs. Furthermore, the SS-GANS performed much better than GANS on the DOIC problem, even without the SOMs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge