Conformal Risk Control for Pulmonary Nodule Detection

Quantitative tools are increasingly appealing for decision support in healthcare, driven by the growing capabilities of advanced AI systems. However, understanding the predictive uncertainties surrounding a tool's output is crucial for decision-makers to ensure reliable and transparent decisions. In this paper, we present a case study on pulmonary nodule detection for lung cancer screening, enhancing an advanced detection model with an uncertainty quantification technique called conformal risk control (CRC). We demonstrate that prediction sets with conformal guarantees are attractive measures of predictive uncertainty in the safety-critical healthcare domain, allowing end-users to achieve arbitrary validity by trading off false positives and providing formal statistical guarantees on model performance. Among ground-truth nodules annotated by at least three radiologists, our model achieves a sensitivity that is competitive with that generally achieved by individual radiologists, with a slight increase in false positives. Furthermore, we illustrate the risks of using off-the-shelve prediction models when faced with ontological uncertainty, such as when radiologists disagree on what constitutes the ground truth on pulmonary nodules.

Distribution-Free Finite-Sample Guarantees and Split Conformal Prediction

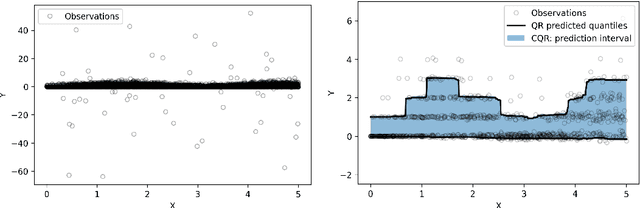
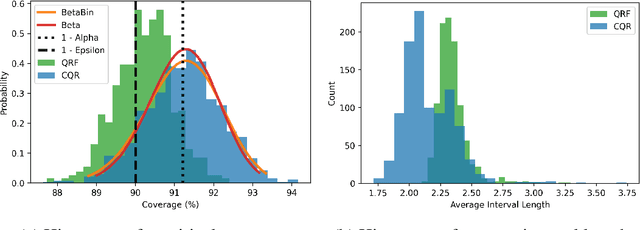
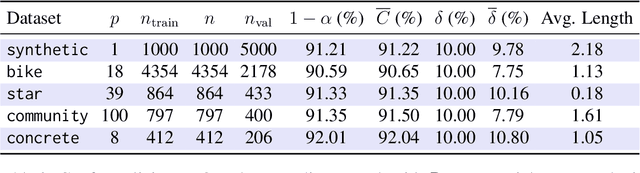
Modern black-box predictive models are often accompanied by weak performance guarantees that only hold asymptotically in the size of the dataset or require strong parametric assumptions. In response to this, split conformal prediction represents a promising avenue to obtain finite-sample guarantees under minimal distribution-free assumptions. Although prediction set validity most often concerns marginal coverage, we explore the related but different guarantee of tolerance regions, reformulating known results in the language of nested prediction sets and extending on the duality between marginal coverage and tolerance regions. Furthermore, we highlight the connection between split conformal prediction and classical tolerance predictors developed in the 1940s, as well as recent developments in distribution-free risk control. One result that transfers from classical tolerance predictors is that the coverage of a prediction set based on order statistics, conditional on the calibration set, is a random variable stochastically dominating the Beta distribution. We demonstrate the empirical effectiveness of our findings on synthetic and real datasets using a popular split conformal prediction procedure called conformalized quantile regression (CQR).