Distribution-Free Finite-Sample Guarantees and Split Conformal Prediction
Paper and Code
Oct 26, 2022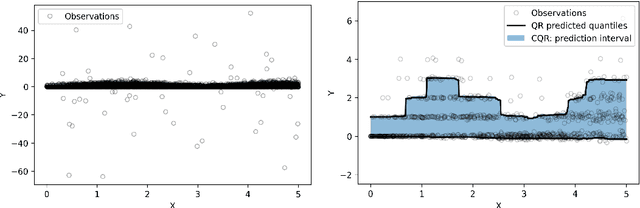

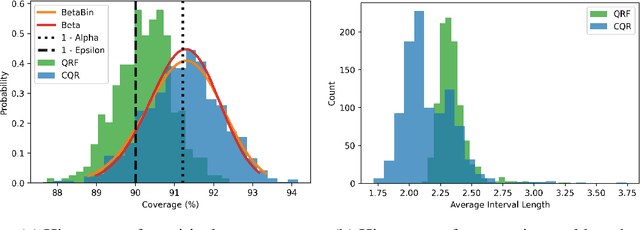
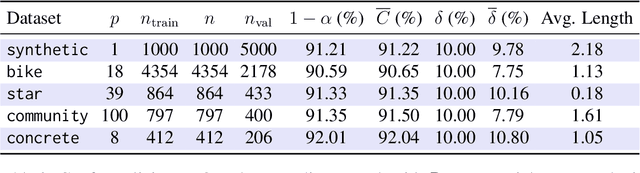
Modern black-box predictive models are often accompanied by weak performance guarantees that only hold asymptotically in the size of the dataset or require strong parametric assumptions. In response to this, split conformal prediction represents a promising avenue to obtain finite-sample guarantees under minimal distribution-free assumptions. Although prediction set validity most often concerns marginal coverage, we explore the related but different guarantee of tolerance regions, reformulating known results in the language of nested prediction sets and extending on the duality between marginal coverage and tolerance regions. Furthermore, we highlight the connection between split conformal prediction and classical tolerance predictors developed in the 1940s, as well as recent developments in distribution-free risk control. One result that transfers from classical tolerance predictors is that the coverage of a prediction set based on order statistics, conditional on the calibration set, is a random variable stochastically dominating the Beta distribution. We demonstrate the empirical effectiveness of our findings on synthetic and real datasets using a popular split conformal prediction procedure called conformalized quantile regression (CQR).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge