Linear Simple Cycle Reservoirs at the edge of stability perform Fourier decomposition of the input driving signals

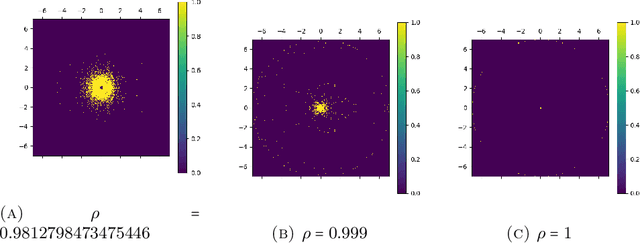
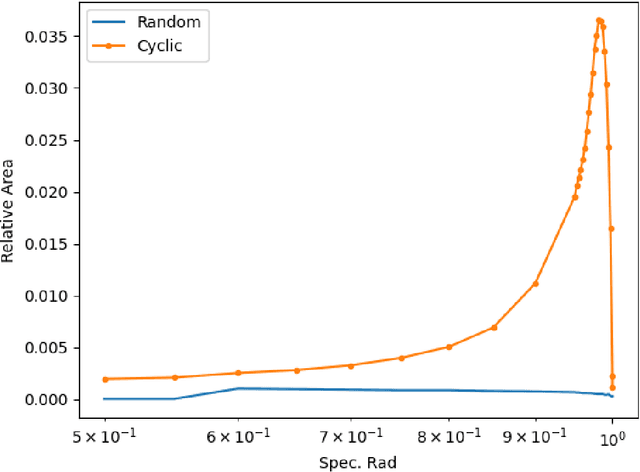
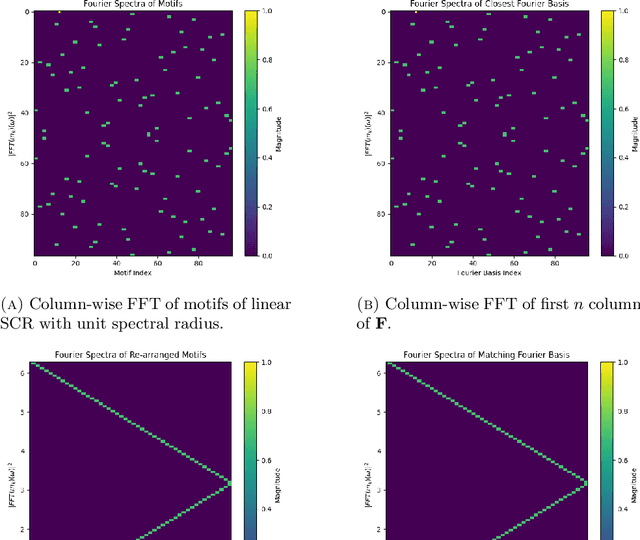
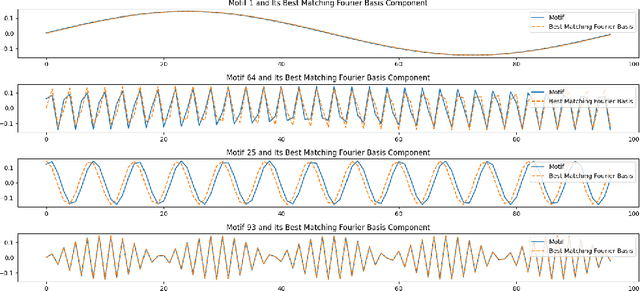
This paper explores the representational structure of linear Simple Cycle Reservoirs (SCR) operating at the edge of stability. We view SCR as providing in their state space feature representations of the input-driving time series. By endowing the state space with the canonical dot-product, we ``reverse engineer" the corresponding kernel (inner product) operating in the original time series space. The action of this time-series kernel is fully characterized by the eigenspace of the corresponding metric tensor. We demonstrate that when linear SCRs are constructed at the edge of stability, the eigenvectors of the time-series kernel align with the Fourier basis. This theoretical insight is supported by numerical experiments.

Universality of Real Minimal Complexity Reservoir

Reservoir Computing (RC) models, a subclass of recurrent neural networks, are distinguished by their fixed, non-trainable input layer and dynamically coupled reservoir, with only the static readout layer being trained. This design circumvents the issues associated with backpropagating error signals through time, thereby enhancing both stability and training efficiency. RC models have been successfully applied across a broad range of application domains. Crucially, they have been demonstrated to be universal approximators of time-invariant dynamic filters with fading memory, under various settings of approximation norms and input driving sources. Simple Cycle Reservoirs (SCR) represent a specialized class of RC models with a highly constrained reservoir architecture, characterized by uniform ring connectivity and binary input-to-reservoir weights with an aperiodic sign pattern. For linear reservoirs, given the reservoir size, the reservoir construction has only one degree of freedom -- the reservoir cycle weight. Such architectures are particularly amenable to hardware implementations without significant performance degradation in many practical tasks. In this study we endow these observations with solid theoretical foundations by proving that SCRs operating in real domain are universal approximators of time-invariant dynamic filters with fading memory. Our results supplement recent research showing that SCRs in the complex domain can approximate, to arbitrary precision, any unrestricted linear reservoir with a non-linear readout. We furthermore introduce a novel method to drastically reduce the number of SCR units, making such highly constrained architectures natural candidates for low-complexity hardware implementations. Our findings are supported by empirical studies on real-world time series datasets.

Predictive Modeling in the Reservoir Kernel Motif Space

This work proposes a time series prediction method based on the kernel view of linear reservoirs. In particular, the time series motifs of the reservoir kernel are used as representational basis on which general readouts are constructed. We provide a geometric interpretation of our approach shedding light on how our approach is related to the core reservoir models and in what way the two approaches differ. Empirical experiments then compare predictive performances of our suggested model with those of recent state-of-art transformer based models, as well as the established recurrent network model - LSTM. The experiments are performed on both univariate and multivariate time series and with a variety of prediction horizons. Rather surprisingly we show that even when linear readout is employed, our method has the capacity to outperform transformer models on univariate time series and attain competitive results on multivariate benchmark datasets. We conclude that simple models with easily controllable capacity but capturing enough memory and subsequence structure can outperform potentially over-complicated deep learning models. This does not mean that reservoir motif based models are preferable to other more complex alternatives - rather, when introducing a new complex time series model one should employ as a sanity check simple, but potentially powerful alternatives/baselines such as reservoir models or the models introduced here.

Simple Cycle Reservoirs are Universal

Reservoir computation models form a subclass of recurrent neural networks with fixed non-trainable input and dynamic coupling weights. Only the static readout from the state space (reservoir) is trainable, thus avoiding the known problems with propagation of gradient information backwards through time. Reservoir models have been successfully applied in a variety of tasks and were shown to be universal approximators of time-invariant fading memory dynamic filters under various settings. Simple cycle reservoirs (SCR) have been suggested as severely restricted reservoir architecture, with equal weight ring connectivity of the reservoir units and input-to-reservoir weights of binary nature with the same absolute value. Such architectures are well suited for hardware implementations without performance degradation in many practical tasks. In this contribution, we rigorously study the expressive power of SCR in the complex domain and show that they are capable of universal approximation of any unrestricted linear reservoir system (with continuous readout) and hence any time-invariant fading memory filter over uniformly bounded input streams.