Rishu Verma
Large Language Models for Mathematical Reasoning: Progresses and Challenges
Jan 31, 2024Abstract:Mathematical reasoning serves as a cornerstone for assessing the fundamental cognitive capabilities of human intelligence. In recent times, there has been a notable surge in the development of Large Language Models (LLMs) geared towards the automated resolution of mathematical problems. However, the landscape of mathematical problem types is vast and varied, with LLM-oriented techniques undergoing evaluation across diverse datasets and settings. This diversity makes it challenging to discern the true advancements and obstacles within this burgeoning field. This survey endeavors to address four pivotal dimensions: i) a comprehensive exploration of the various mathematical problems and their corresponding datasets that have been investigated; ii) an examination of the spectrum of LLM-oriented techniques that have been proposed for mathematical problem-solving; iii) an overview of factors and concerns affecting LLMs in solving math; and iv) an elucidation of the persisting challenges within this domain. To the best of our knowledge, this survey stands as one of the first extensive examinations of the landscape of LLMs in the realm of mathematics, providing a holistic perspective on the current state, accomplishments, and future challenges in this rapidly evolving field.
Analysis of different temporal graph neural network configurations on dynamic graphs
May 02, 2023
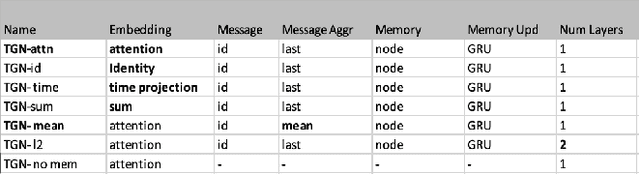
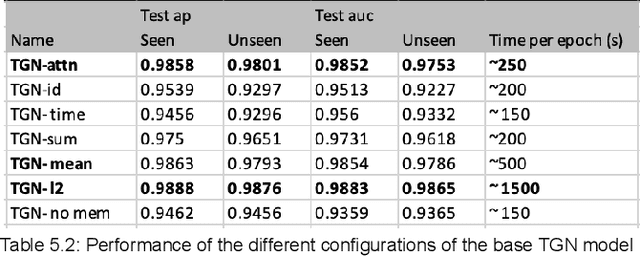
Abstract:In recent years, there has been an increasing interest in the use of graph neural networks (GNNs) for analyzing dynamic graphs, which are graphs that evolve over time. However, there is still a lack of understanding of how different temporal graph neural network (TGNs) configurations can impact the accuracy of predictions on dynamic graphs. Moreover, the hunt for benchmark datasets for these TGNs models is still ongoing. Up until recently, Pytorch Geometric Temporal came up with a few benchmark datasets but most of these datasets have not been analyzed with different TGN models to establish the state-of-the-art. Therefore, this project aims to address this gap in the literature by performing a qualitative analysis of spatial-temporal dependence structure learning on dynamic graphs, as well as a comparative study of the effectiveness of selected TGNs on node and edge prediction tasks. Additionally, an extensive ablation study will be conducted on different variants of the best-performing TGN to identify the key factors contributing to its performance. By achieving these objectives, this project will provide valuable insights into the design and optimization of TGNs for dynamic graph analysis, with potential applications in areas such as disease spread prediction, social network analysis, traffic prediction, and more. Moreover, an attempt is made to convert snapshot-based data to the event-based dataset and make it compatible with the SOTA model namely TGN to perform node regression task.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge