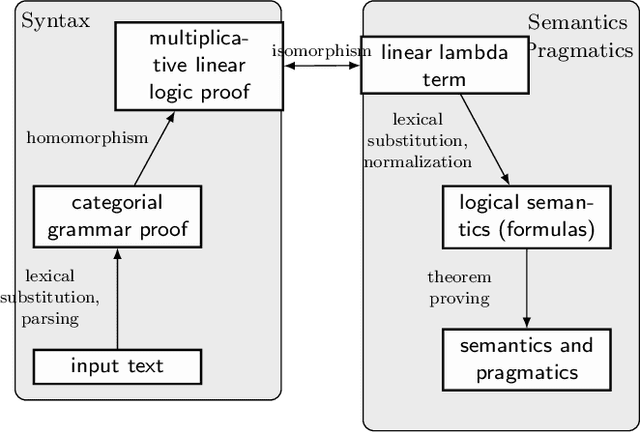
SPINDLE: Spinning Raw Text into Lambda Terms with Graph Attention

This paper describes SPINDLE - an open source Python module implementing an efficient and accurate parser for written Dutch that transforms raw text input to programs for meaning composition, expressed as {\lambda} terms. The parser integrates a number of breakthrough advances made in recent years. Its output consists of hi-res derivations of a multimodal type-logical grammar, capturing two orthogonal axes of syntax, namely deep function-argument structures and dependency relations. These are produced by three interdependent systems: a static type-checker asserting the well-formedness of grammatical analyses, a state-of-the-art, structurally-aware supertagger based on heterogeneous graph convolutions, and a massively parallel proof search component based on Sinkhorn iterations. Packed in the software are also handy utilities and extras for proof visualization and inference, intended to facilitate end-user utilization.

Perspectives on neural proof nets

In this paper I will present a novel way of combining proof net proof search with neural networks. It contrasts with the 'standard' approach which has been applied to proof search in type-logical grammars in various different forms. In the standard approach, we first transform words to formulas (supertagging) then match atomic formulas to obtain a proof. I will introduce an alternative way to split the task into two: first, we generate the graph structure in a way which guarantees it corresponds to a lambda-term, then we obtain the detailed structure using vertex labelling. Vertex labelling is a well-studied task in graph neural networks, and different ways of implementing graph generation using neural networks will be explored.

Proof-theoretic aspects of NL$λ$

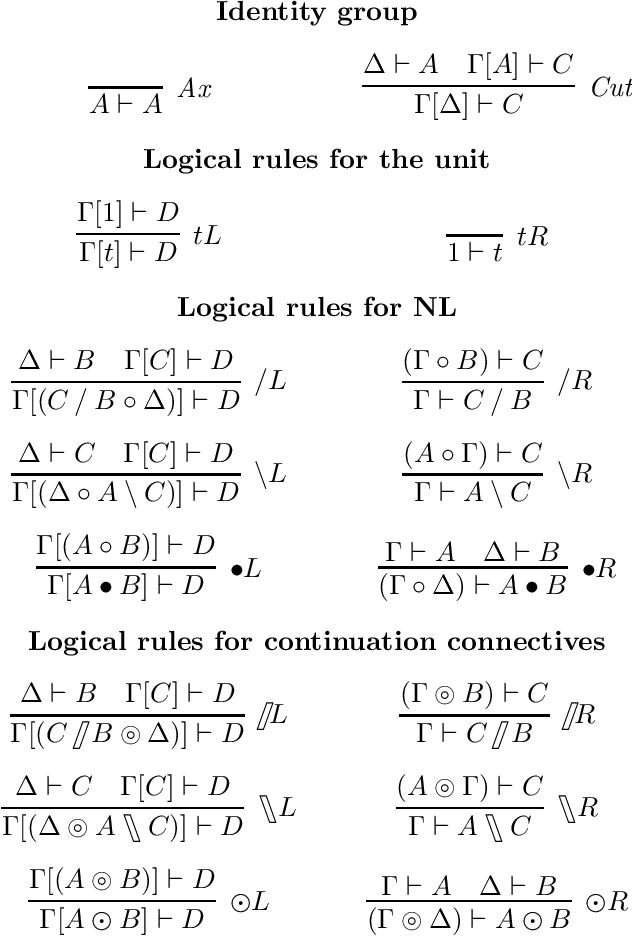
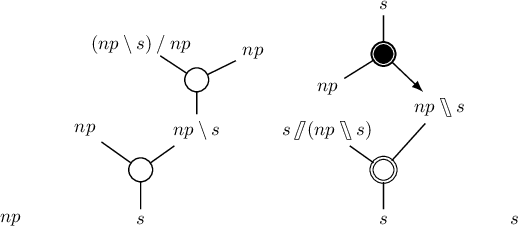
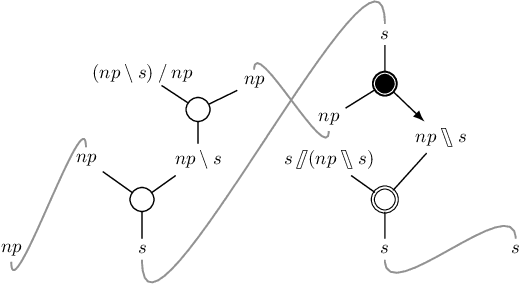
We present a proof-theoretic analysis of the logic NL$\lambda$ (Barker \& Shan 2014, Barker 2019). We notably introduce a novel calculus of proof nets and prove it is sound and complete with respect to the sequent calculus for the logic. We study decidability and complexity of the logic using this new calculus, proving a new upper bound for complexity of the logic (showing it is in NP) and a new lower bound for the class of formal language generated by the formalism (mildly context-sensitive languages extended with a permutation closure operation). Finally, thanks to this new calculus, we present a novel comparison between NL$\lambda$ and the hybrid type-logical grammars of Kubota \& Levine (2020). We show there is an unexpected convergence of the natural language analyses proposed in the two formalism. In addition to studying the proof-theoretic properties of NL$\lambda$, we greatly extends its linguistic coverage.

Neural Proof Nets

Linear logic and the linear {\lambda}-calculus have a long standing tradition in the study of natural language form and meaning. Among the proof calculi of linear logic, proof nets are of particular interest, offering an attractive geometric representation of derivations that is unburdened by the bureaucratic complications of conventional prooftheoretic formats. Building on recent advances in set-theoretic learning, we propose a neural variant of proof nets based on Sinkhorn networks, which allows us to translate parsing as the problem of extracting syntactic primitives and permuting them into alignment. Our methodology induces a batch-efficient, end-to-end differentiable architecture that actualizes a formally grounded yet highly efficient neuro-symbolic parser. We test our approach on {\AE}Thel, a dataset of type-logical derivations for written Dutch, where it manages to correctly transcribe raw text sentences into proofs and terms of the linear {\lambda}-calculus with an accuracy of as high as 70%.

Logical foundations for hybrid type-logical grammars

This paper explores proof-theoretic aspects of hybrid type-logical grammars , a logic combining Lambek grammars with lambda grammars. We prove some basic properties of the calculus, such as normalisation and the subformula property and also present both a sequent and a proof net calculus for hybrid type-logical grammars. In addition to clarifying the logical foundations of hybrid type-logical grammars, the current study opens the way to variants and extensions of the original system, including but not limited to a non-associative version and a multimodal version incorporating structural rules and unary modes.

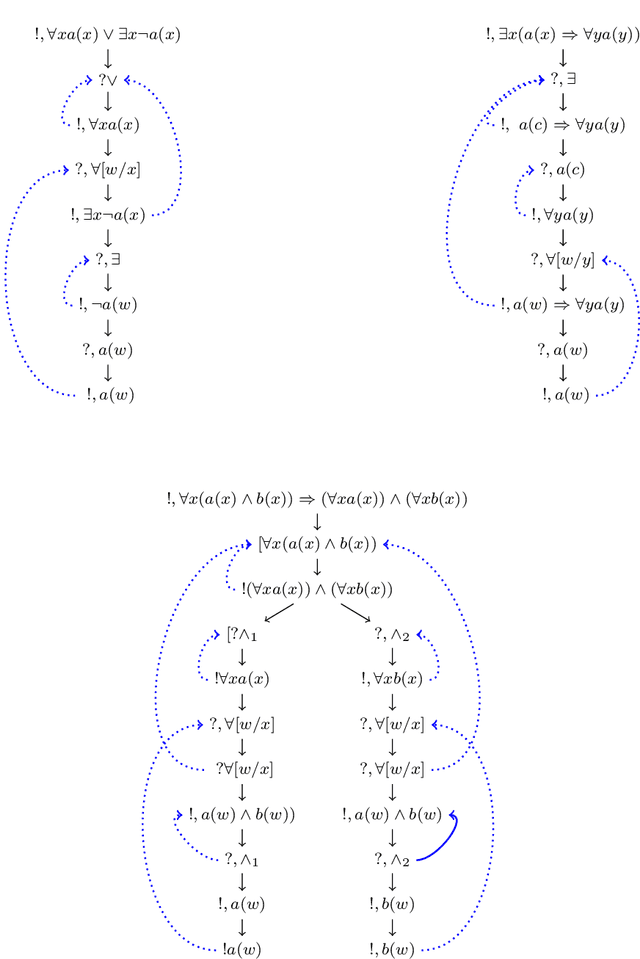
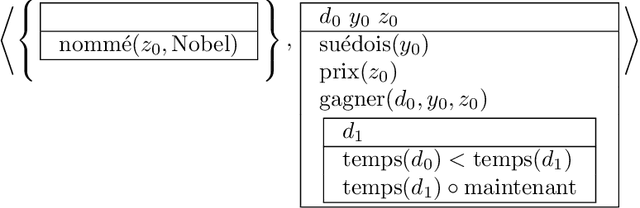
Logical Semantics, Dialogical Argumentation, and Textual Entailment

In this chapter, we introduce a new dialogical system for first order classical logic which is close to natural language argumentation, and we prove its completeness with respect to usual classical validity. We combine our dialogical system with the Grail syntactic and semantic parser developed by the second author in order to address automated textual entailment, that is, we use it for deciding whether or not a sentence is a consequence of a short text. This work-which connects natural language semantics and argumentation with dialogical logic-can be viewed as a step towards an inferentialist view of natural language semantics.

Partial Orders, Residuation, and First-Order Linear Logic

We will investigate proof-theoretic and linguistic aspects of first-order linear logic. We will show that adding partial order constraints in such a way that each sequent defines a unique linear order on the antecedent formulas of a sequent allows us to define many useful logical operators. In addition, the partial order constraints improve the efficiency of proof search.

ÆTHEL: Automatically Extracted Type-Logical Derivations for Dutch

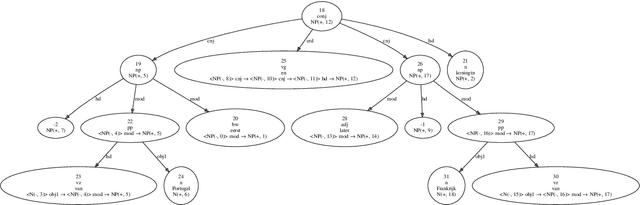
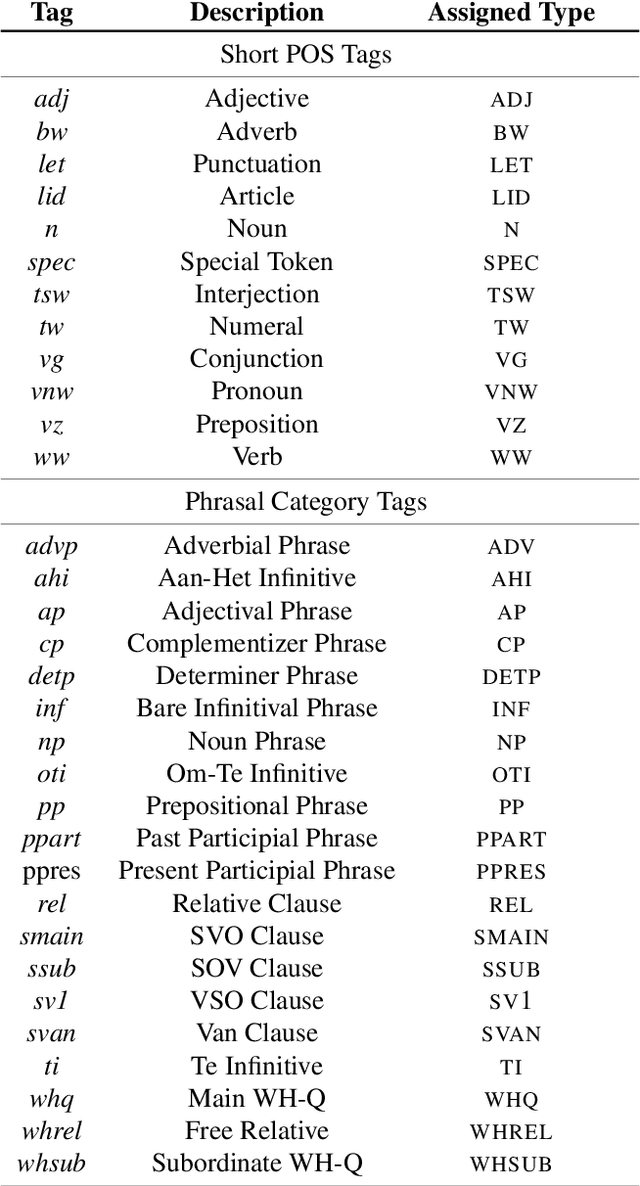
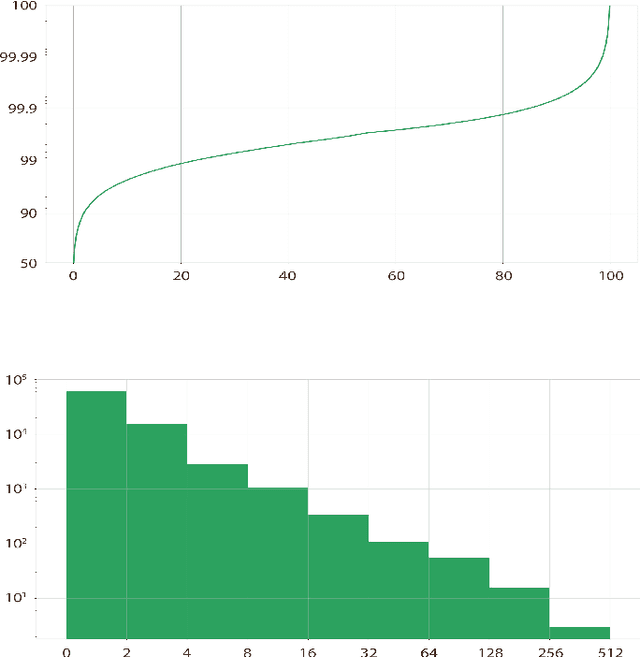
We present {\AE}THEL, a semantic compositionality dataset for written Dutch. {\AE}THEL consists of two parts. First, it contains a lexicon of supertags for about 900,000 words in context. The supertags correspond to types of the simply typed linear lambda-calculus, enhanced with dependency decorations that capture grammatical roles supplementary to function-argument structures. On the basis of these types, {\AE}THEL further provides 72,623 validated derivations, presented in four equivalent formats: natural-deduction and sequent-style proofs, linear logic proofnets and the associated programs (lambda terms) for meaning composition. {\AE}THEL's types and derivations are obtained by means of an extraction algorithm applied to the syntactic analyses of LASSY-Small, the gold standard corpus of written Dutch. We discuss the extraction algorithm and show how `virtual elements' in the original LASSY annotation of unbounded dependencies and coordination phenomena give rise to higher-order types. We suggest some example usecases highlighting the benefits of a type-driven approach at the syntax semantics interface. The following resources are open-sourced with {\AE}THEL: the lexical mappings between words and types, a subset of the dataset consisting of 8,569 semantic parses, and the Python code that implements the extraction algorithm.

Chart Parsing Multimodal Grammars

The short note describes the chart parser for multimodal type-logical grammars which has been developed in conjunction with the type-logical treebank for French. The chart parser presents an incomplete but fast implementation of proof search for multimodal type-logical grammars using the "deductive parsing" framework. Proofs found can be transformed to natural deduction proofs.

The Grail theorem prover: Type theory for syntax and semantics

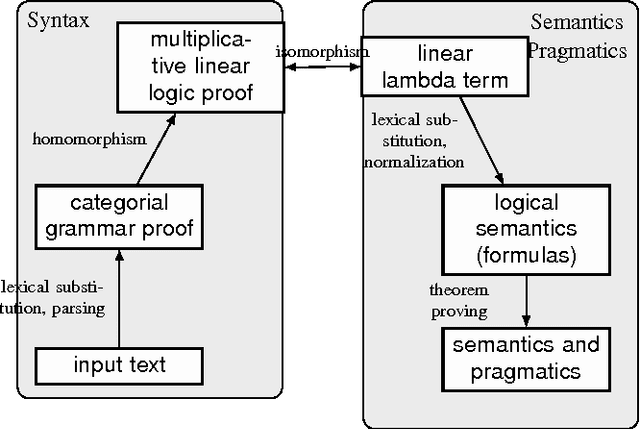
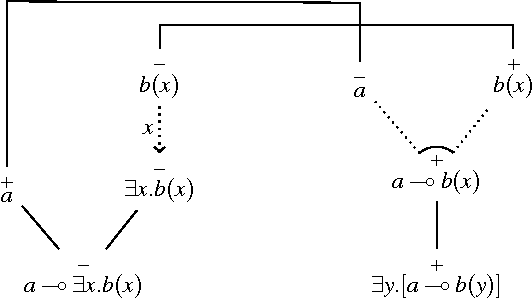
As the name suggests, type-logical grammars are a grammar formalism based on logic and type theory. From the prespective of grammar design, type-logical grammars develop the syntactic and semantic aspects of linguistic phenomena hand-in-hand, letting the desired semantics of an expression inform the syntactic type and vice versa. Prototypical examples of the successful application of type-logical grammars to the syntax-semantics interface include coordination, quantifier scope and extraction.This chapter describes the Grail theorem prover, a series of tools for designing and testing grammars in various modern type-logical grammars which functions as a tool . All tools described in this chapter are freely available.