Proof-theoretic aspects of NL$λ$
Paper and Code
Oct 23, 2020
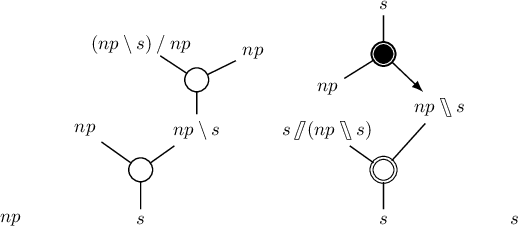

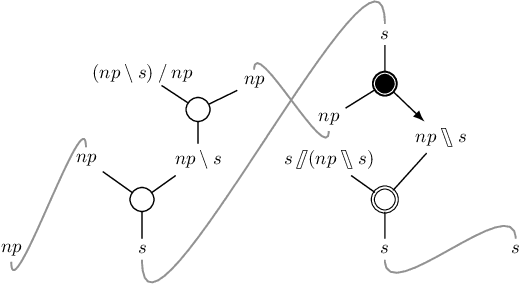
We present a proof-theoretic analysis of the logic NL$\lambda$ (Barker \& Shan 2014, Barker 2019). We notably introduce a novel calculus of proof nets and prove it is sound and complete with respect to the sequent calculus for the logic. We study decidability and complexity of the logic using this new calculus, proving a new upper bound for complexity of the logic (showing it is in NP) and a new lower bound for the class of formal language generated by the formalism (mildly context-sensitive languages extended with a permutation closure operation). Finally, thanks to this new calculus, we present a novel comparison between NL$\lambda$ and the hybrid type-logical grammars of Kubota \& Levine (2020). We show there is an unexpected convergence of the natural language analyses proposed in the two formalism. In addition to studying the proof-theoretic properties of NL$\lambda$, we greatly extends its linguistic coverage.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge