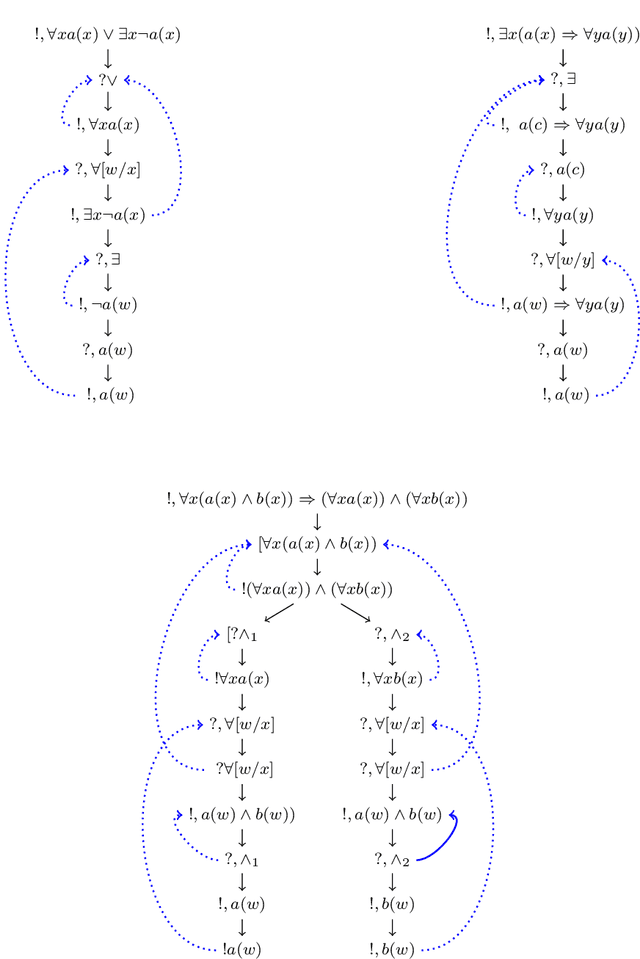
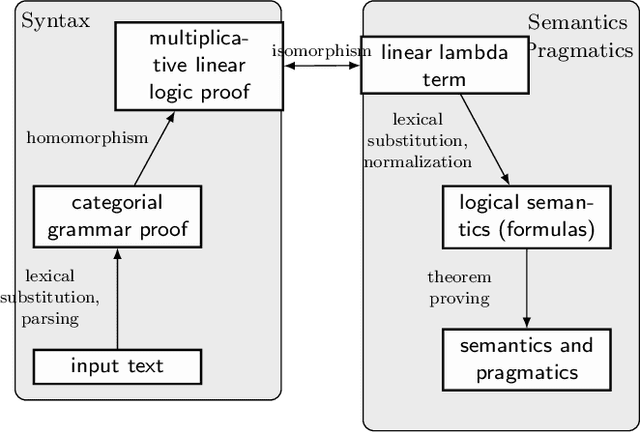
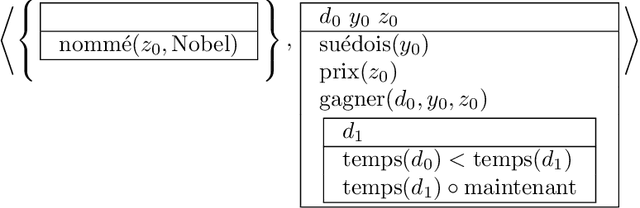
Logical Semantics, Dialogical Argumentation, and Textual Entailment

In this chapter, we introduce a new dialogical system for first order classical logic which is close to natural language argumentation, and we prove its completeness with respect to usual classical validity. We combine our dialogical system with the Grail syntactic and semantic parser developed by the second author in order to address automated textual entailment, that is, we use it for deciding whether or not a sentence is a consequence of a short text. This work-which connects natural language semantics and argumentation with dialogical logic-can be viewed as a step towards an inferentialist view of natural language semantics.

Natural Language Semantics and Computability

This paper is a reflexion on the computability of natural language semantics. It does not contain a new model or new results in the formal semantics of natural language: it is rather a computational analysis of the logical models and algorithms currently used in natural language semantics, defined as the mapping of a statement to logical formulas - formulas, because a statement can be ambiguous. We argue that as long as possible world semantics is left out, one can compute the semantic representation(s) of a given statement, including aspects of lexical meaning. We also discuss the algorithmic complexity of this process.

Typed Hilbert Epsilon Operators and the Semantics of Determiner Phrases (Invited Lecture)

The semantics of determiner phrases, be they definite de- scriptions, indefinite descriptions or quantified noun phrases, is often as- sumed to be a fully solved question: common nouns are properties, and determiners are generalised quantifiers that apply to two predicates: the property corresponding to the common noun and the one corresponding to the verb phrase. We first present a criticism of this standard view. Firstly, the semantics of determiners does not follow the syntactical structure of the sentence. Secondly the standard interpretation of the indefinite article cannot ac- count for nominal sentences. Thirdly, the standard view misses the linguis- tic asymmetry between the two properties of a generalised quantifier. In the sequel, we propose a treatment of determiners and quantifiers as Hilbert terms in a richly typed system that we initially developed for lexical semantics, using a many sorted logic for semantical representations. We present this semantical framework called the Montagovian generative lexicon and show how these terms better match the syntactical structure and avoid the aforementioned problems of the standard approach. Hilbert terms rather differ from choice functions in that there is one polymorphic operator and not one operator per formula. They also open an intriguing connection between the logic for meaning assembly, the typed lambda calculus handling compositionality and the many-sorted logic for semantical representations. Furthermore epsilon terms naturally introduce type-judgements and confirm the claim that type judgment are a form of presupposition.

Category theory, logic and formal linguistics: some connections, old and new

We seize the opportunity of the publication of selected papers from the \emph{Logic, categories, semantics} workshop in the \emph{Journal of Applied Logic} to survey some current trends in logic, namely intuitionistic and linear type theories, that interweave categorical, geometrical and computational considerations. We thereafter present how these rich logical frameworks can model the way language conveys meaning.

Deverbal semantics and the Montagovian generative lexicon

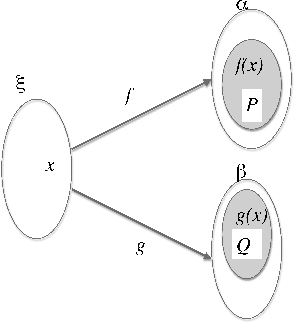
We propose a lexical account of action nominals, in particular of deverbal nominalisations, whose meaning is related to the event expressed by their base verb. The literature about nominalisations often assumes that the semantics of the base verb completely defines the structure of action nominals. We argue that the information in the base verb is not sufficient to completely determine the semantics of action nominals. We exhibit some data from different languages, especially from Romance language, which show that nominalisations focus on some aspects of the verb semantics. The selected aspects, however, seem to be idiosyncratic and do not automatically result from the internal structure of the verb nor from its interaction with the morphological suffix. We therefore propose a partially lexicalist approach view of deverbal nouns. It is made precise and computable by using the Montagovian Generative Lexicon, a type theoretical framework introduced by Bassac, Mery and Retor\'e in this journal in 2010. This extension of Montague semantics with a richer type system easily incorporates lexical phenomena like the semantics of action nominals in particular deverbals, including their polysemy and (in)felicitous copredications.

A type theoretical framework for natural language semantics: the Montagovian generative lexicon

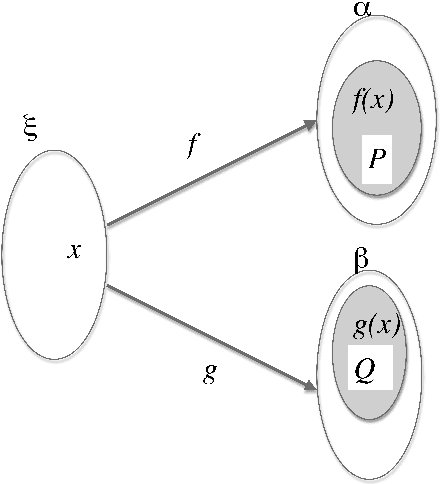
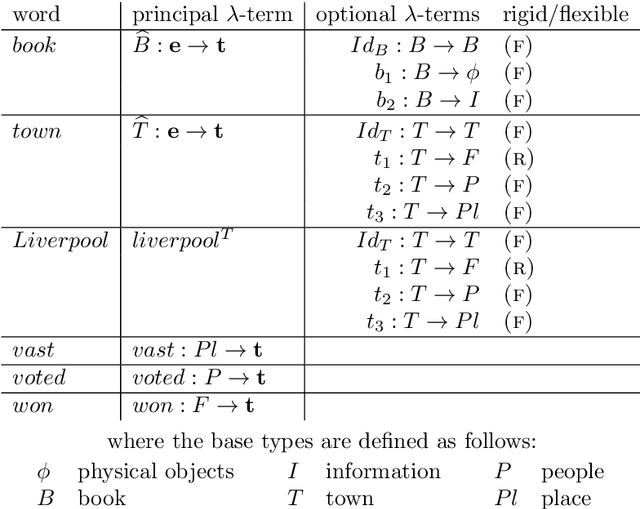
We present a framework, named the Montagovian generative lexicon, for computing the semantics of natural language sentences, expressed in many sorted higher order logic. Word meaning is depicted by lambda terms of second order lambda calculus (Girard's system F) with base types including a type for propositions and many types for sorts of a many sorted logic. This framework is able to integrate a proper treatment of lexical phenomena into a Montagovian compositional semantics, including the restriction of selection which imposes the nature of the arguments of a predicate, and the possible adaptation of a word meaning to some contexts. Among these adaptations of a word's sense to the context, ontological inclusions are handled by an extension of system F with coercive subtyping that is introduced in the present paper. The benefits of this framework for lexical pragmatics are illustrated on meaning transfers and coercions, on possible and impossible copredication over different senses, on deverbal ambiguities, and on "fictive motion". Next we show that the compositional treatment of determiners, quantifiers, plurals,... are finer grained in our framework. We then conclude with the linguistic, logical and computational perspectives opened by the Montagovian generative lexicon.

Plurals: individuals and sets in a richly typed semantics

We developed a type-theoretical framework for natural lan- guage semantics that, in addition to the usual Montagovian treatment of compositional semantics, includes a treatment of some phenomena of lex- ical semantic: coercions, meaning, transfers, (in)felicitous co-predication. In this setting we see how the various readings of plurals (collective, dis- tributive, coverings,...) can be modelled.

Semantic Types, Lexical Sorts and Classifiers

We propose a cognitively and linguistically motivated set of sorts for lexical semantics in a compositional setting: the classifiers in languages that do have such pronouns. These sorts are needed to include lexical considerations in a semantical analyser such as Boxer or Grail. Indeed, all proposed lexical extensions of usual Montague semantics to model restriction of selection, felicitous and infelicitous copredication require a rich and refined type system whose base types are the lexical sorts, the basis of the many-sorted logic in which semantical representations of sentences are stated. However, none of those approaches define precisely the actual base types or sorts to be used in the lexicon. In this article, we shall discuss some of the options commonly adopted by researchers in formal lexical semantics, and defend the view that classifiers in the languages which have such pronouns are an appealing solution, both linguistically and cognitively motivated.

Logique mathématique et linguistique formelle

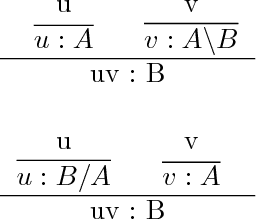
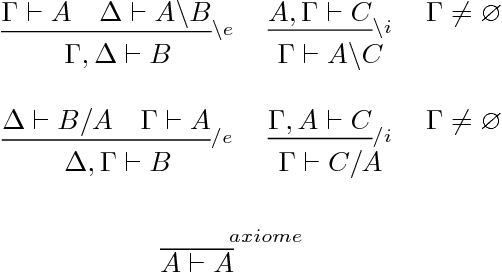
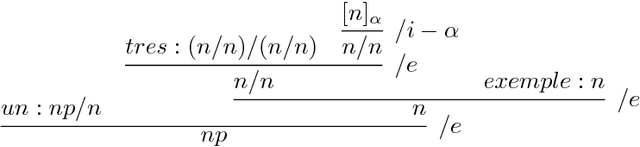
As the etymology of the word shows, logic is intimately related to language, as exemplified by the work of philosophers from Antiquity and from the Middle-Age. At the beginning of the XX century, the crisis of the foundations of mathematics invented mathematical logic and imposed logic as a language-based foundation for mathematics. How did the relations between logic and language evolved in this newly defined mathematical framework? After a survey of the history of the relation between logic and linguistics, traditionally focused on semantics, we focus on some present issues: 1) grammar as a deductive system 2) the transformation of the syntactic structure of a sentence to a logical formula representing its meaning 3) taking into account the context when interpreting words. This lecture shows that type theory provides a convenient framework both for natural language syntax and for the interpretation of any of tis level (words, sentences, discourse).

Learning Lambek grammars from proof frames

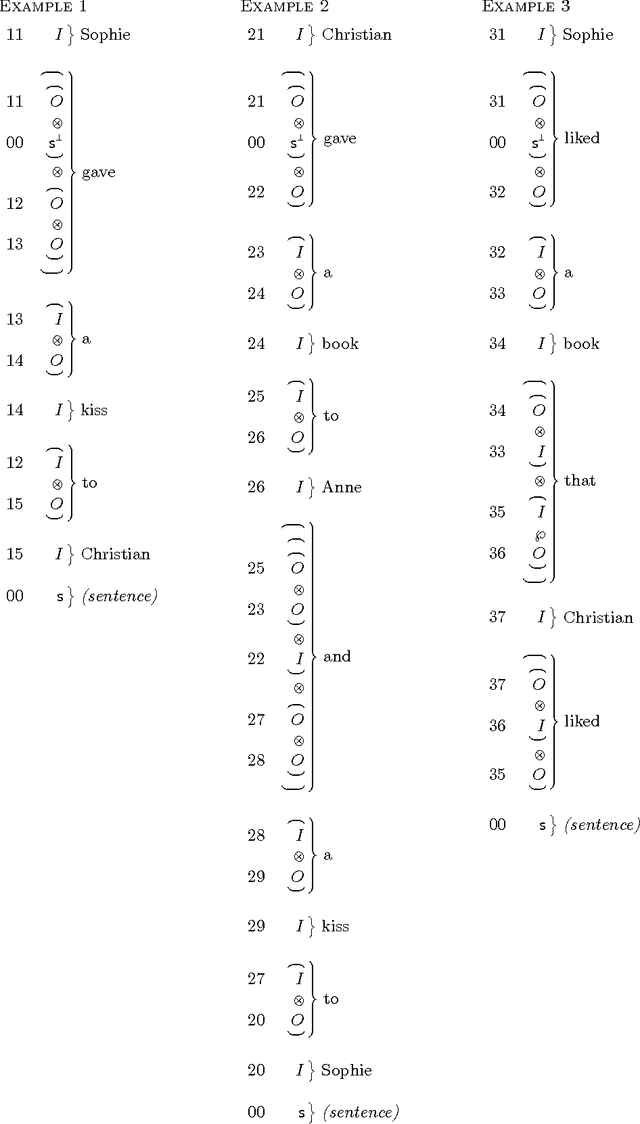
In addition to their limpid interface with semantics, categorial grammars enjoy another important property: learnability. This was first noticed by Buskowsky and Penn and further studied by Kanazawa, for Bar-Hillel categorial grammars. What about Lambek categorial grammars? In a previous paper we showed that product free Lambek grammars where learnable from structured sentences, the structures being incomplete natural deductions. These grammars were shown to be unlearnable from strings by Foret and Le Nir. In the present paper we show that Lambek grammars, possibly with product, are learnable from proof frames that are incomplete proof nets. After a short reminder on grammatical inference \`a la Gold, we provide an algorithm that learns Lambek grammars with product from proof frames and we prove its convergence. We do so for 1-valued also known as rigid Lambek grammars with product, since standard techniques can extend our result to $k$-valued grammars. Because of the correspondence between cut-free proof nets and normal natural deductions, our initial result on product free Lambek grammars can be recovered. We are sad to dedicate the present paper to Philippe Darondeau, with whom we started to study such questions in Rennes at the beginning of the millennium, and who passed away prematurely. We are glad to dedicate the present paper to Jim Lambek for his 90 birthday: he is the living proof that research is an eternal learning process.