Learning Lambek grammars from proof frames

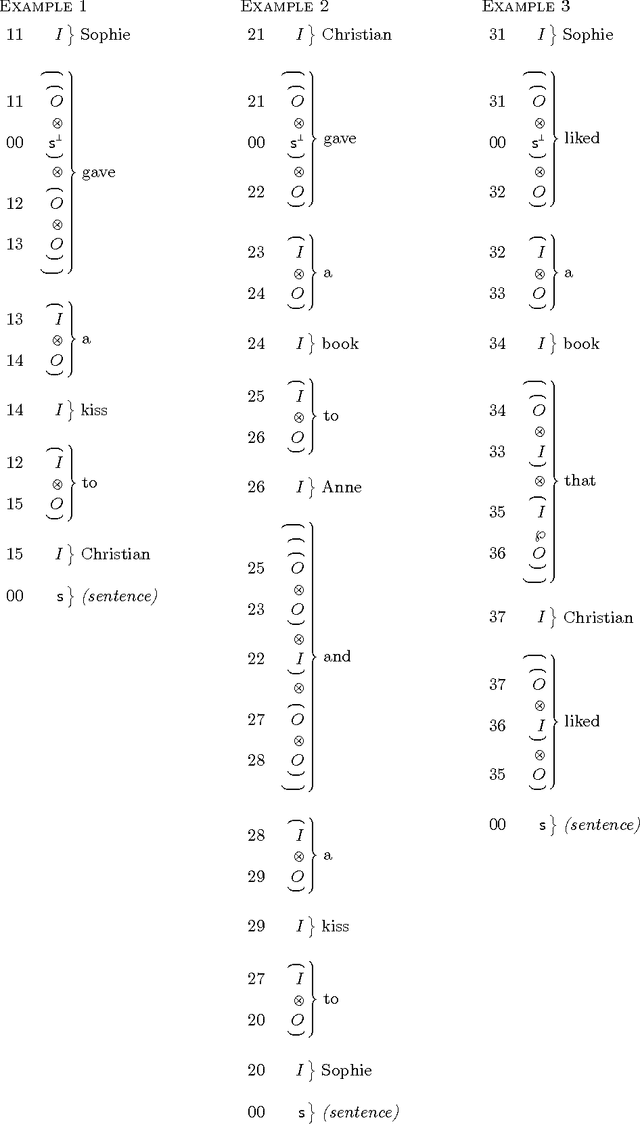
In addition to their limpid interface with semantics, categorial grammars enjoy another important property: learnability. This was first noticed by Buskowsky and Penn and further studied by Kanazawa, for Bar-Hillel categorial grammars. What about Lambek categorial grammars? In a previous paper we showed that product free Lambek grammars where learnable from structured sentences, the structures being incomplete natural deductions. These grammars were shown to be unlearnable from strings by Foret and Le Nir. In the present paper we show that Lambek grammars, possibly with product, are learnable from proof frames that are incomplete proof nets. After a short reminder on grammatical inference \`a la Gold, we provide an algorithm that learns Lambek grammars with product from proof frames and we prove its convergence. We do so for 1-valued also known as rigid Lambek grammars with product, since standard techniques can extend our result to $k$-valued grammars. Because of the correspondence between cut-free proof nets and normal natural deductions, our initial result on product free Lambek grammars can be recovered. We are sad to dedicate the present paper to Philippe Darondeau, with whom we started to study such questions in Rennes at the beginning of the millennium, and who passed away prematurely. We are glad to dedicate the present paper to Jim Lambek for his 90 birthday: he is the living proof that research is an eternal learning process.

A Study on Learnability for Rigid Lambek Grammars

We present basic notions of Gold's "learnability in the limit" paradigm, first presented in 1967, a formalization of the cognitive process by which a native speaker gets to grasp the underlying grammar of his/her own native language by being exposed to well formed sentences generated by that grammar. Then we present Lambek grammars, a formalism issued from categorial grammars which, although not as expressive as needed for a full formalization of natural languages, is particularly suited to easily implement a natural interface between syntax and semantics. In the last part of this work, we present a learnability result for Rigid Lambek grammars from structured examples.