A type theoretical framework for natural language semantics: the Montagovian generative lexicon

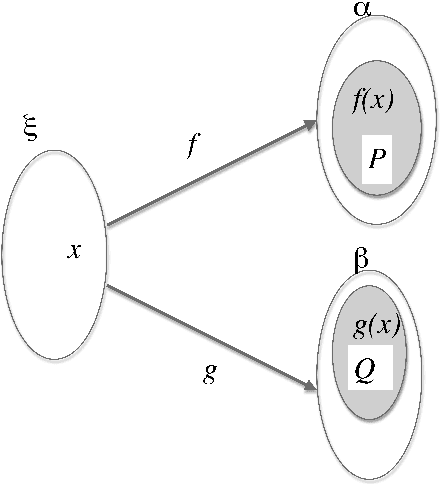
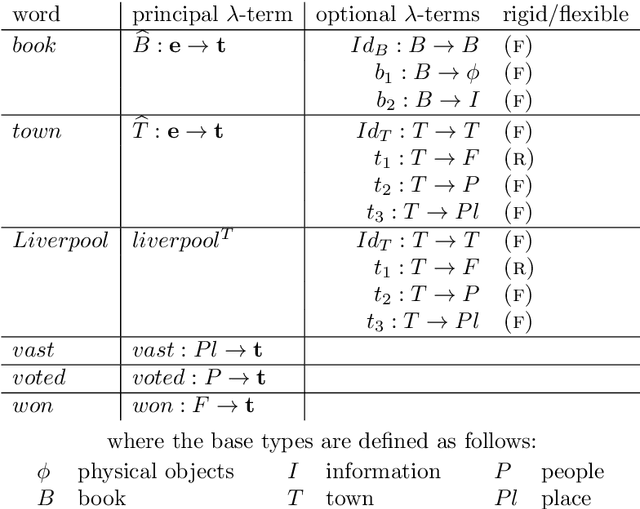
We present a framework, named the Montagovian generative lexicon, for computing the semantics of natural language sentences, expressed in many sorted higher order logic. Word meaning is depicted by lambda terms of second order lambda calculus (Girard's system F) with base types including a type for propositions and many types for sorts of a many sorted logic. This framework is able to integrate a proper treatment of lexical phenomena into a Montagovian compositional semantics, including the restriction of selection which imposes the nature of the arguments of a predicate, and the possible adaptation of a word meaning to some contexts. Among these adaptations of a word's sense to the context, ontological inclusions are handled by an extension of system F with coercive subtyping that is introduced in the present paper. The benefits of this framework for lexical pragmatics are illustrated on meaning transfers and coercions, on possible and impossible copredication over different senses, on deverbal ambiguities, and on "fictive motion". Next we show that the compositional treatment of determiners, quantifiers, plurals,... are finer grained in our framework. We then conclude with the linguistic, logical and computational perspectives opened by the Montagovian generative lexicon.