Gradient-based Filter Design for the Dual-tree Wavelet Transform

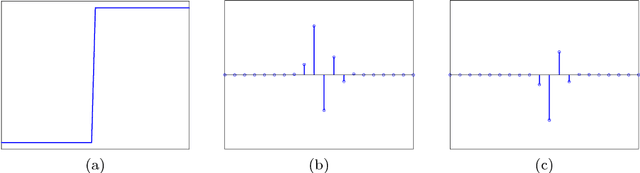
The wavelet transform has seen success when incorporated into neural network architectures, such as in wavelet scattering networks. More recently, it has been shown that the dual-tree complex wavelet transform can provide better representations than the standard transform. With this in mind, we extend our previous method for learning filters for the 1D and 2D wavelet transforms into the dual-tree domain. We show that with few modifications to our original model, we can learn directional filters that leverage the properties of the dual-tree wavelet transform.

Learning Sparse Wavelet Representations

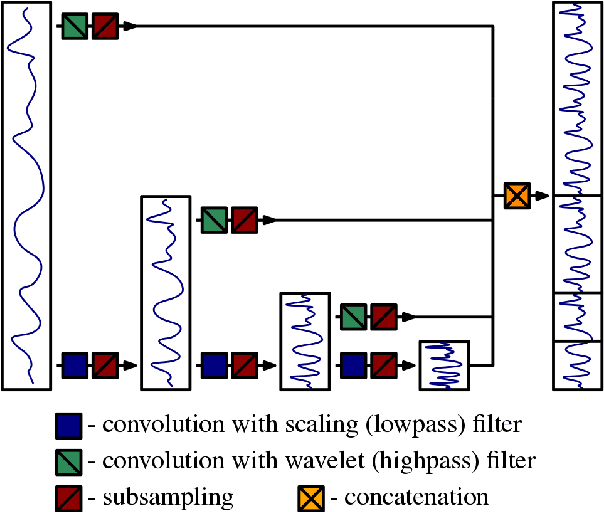
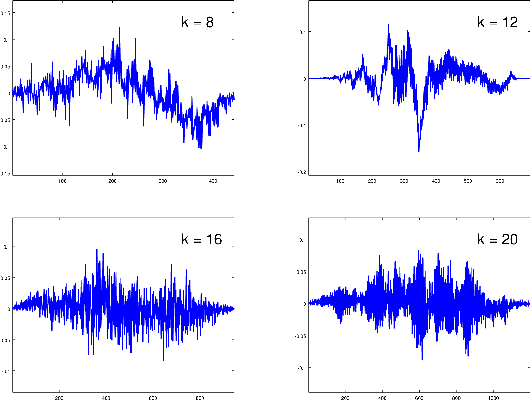
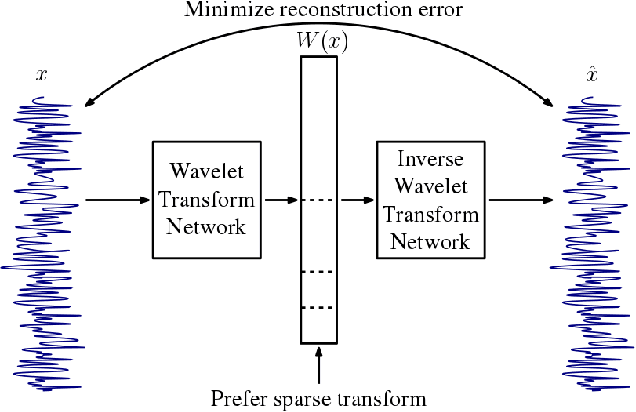
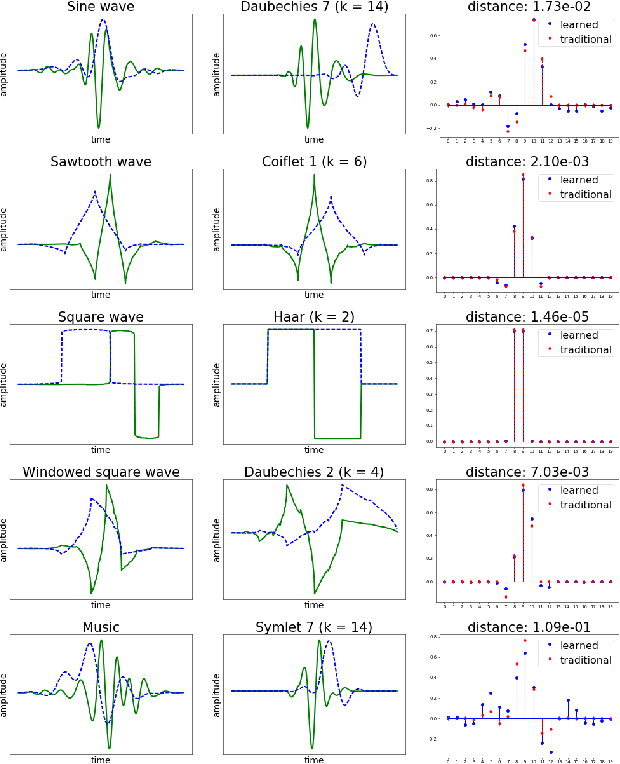
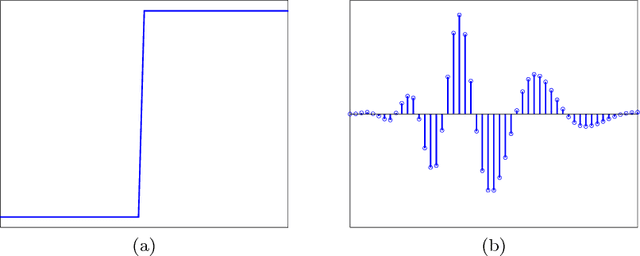
In this work we propose a method for learning wavelet filters directly from data. We accomplish this by framing the discrete wavelet transform as a modified convolutional neural network. We introduce an autoencoder wavelet transform network that is trained using gradient descent. We show that the model is capable of learning structured wavelet filters from synthetic and real data. The learned wavelets are shown to be similar to traditional wavelets that are derived using Fourier methods. Our method is simple to implement and easily incorporated into neural network architectures. A major advantage to our model is that we can learn from raw audio data.

Bayesian Optimal Active Search and Surveying

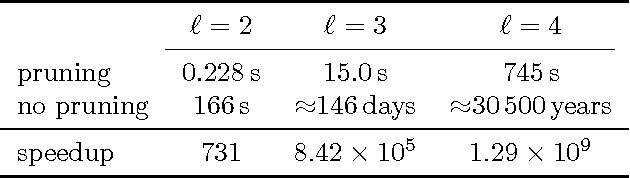
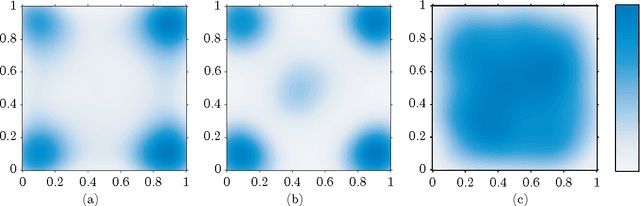
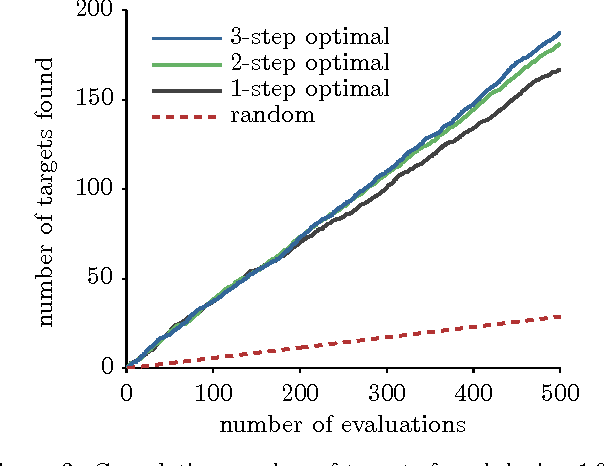
We consider two active binary-classification problems with atypical objectives. In the first, active search, our goal is to actively uncover as many members of a given class as possible. In the second, active surveying, our goal is to actively query points to ultimately predict the proportion of a given class. Numerous real-world problems can be framed in these terms, and in either case typical model-based concerns such as generalization error are only of secondary importance. We approach these problems via Bayesian decision theory; after choosing natural utility functions, we derive the optimal policies. We provide three contributions. In addition to introducing the active surveying problem, we extend previous work on active search in two ways. First, we prove a novel theoretical result, that less-myopic approximations to the optimal policy can outperform more-myopic approximations by any arbitrary degree. We then derive bounds that for certain models allow us to reduce (in practice dramatically) the exponential search space required by a naive implementation of the optimal policy, enabling further lookahead while still ensuring that optimal decisions are always made.