Green Machine Learning via Augmented Gaussian Processes and Multi-Information Source Optimization

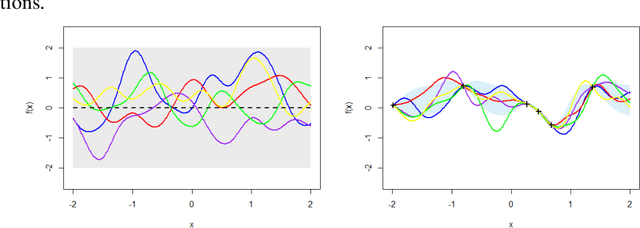
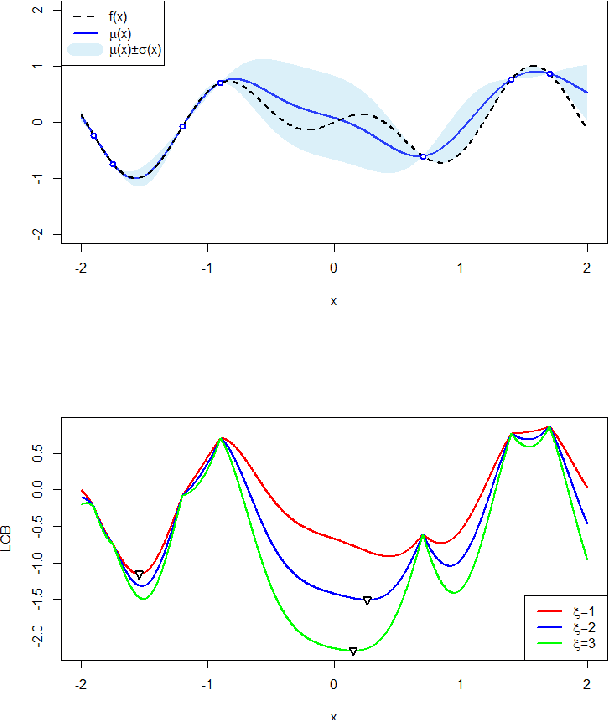
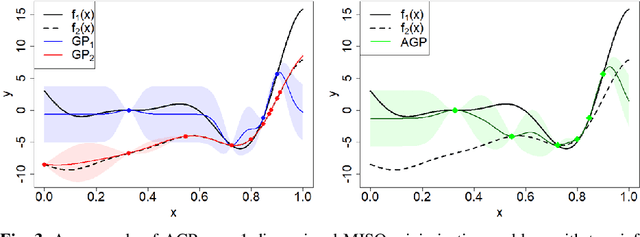
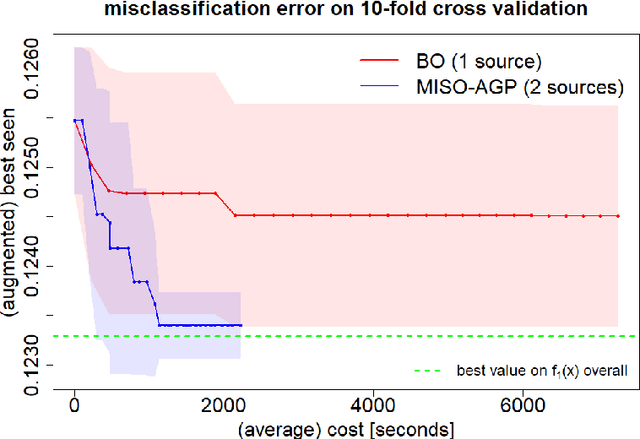
Searching for accurate Machine and Deep Learning models is a computationally expensive and awfully energivorous process. A strategy which has been gaining recently importance to drastically reduce computational time and energy consumed is to exploit the availability of different information sources, with different computational costs and different "fidelity", typically smaller portions of a large dataset. The multi-source optimization strategy fits into the scheme of Gaussian Process based Bayesian Optimization. An Augmented Gaussian Process method exploiting multiple information sources (namely, AGP-MISO) is proposed. The Augmented Gaussian Process is trained using only "reliable" information among available sources. A novel acquisition function is defined according to the Augmented Gaussian Process. Computational results are reported related to the optimization of the hyperparameters of a Support Vector Machine (SVM) classifier using two sources: a large dataset - the most expensive one - and a smaller portion of it. A comparison with a traditional Bayesian Optimization approach to optimize the hyperparameters of the SVM classifier on the large dataset only is reported.

Modelling Human Active Search in Optimizing Black-box Functions

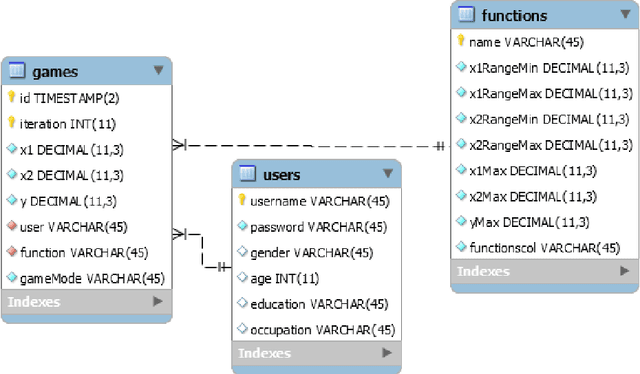
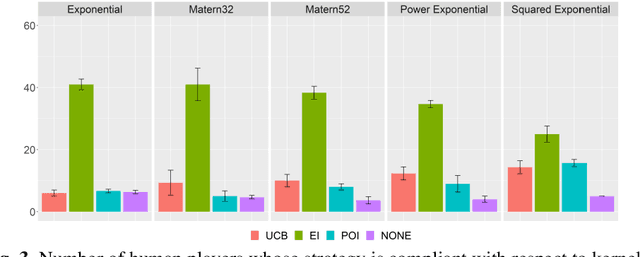
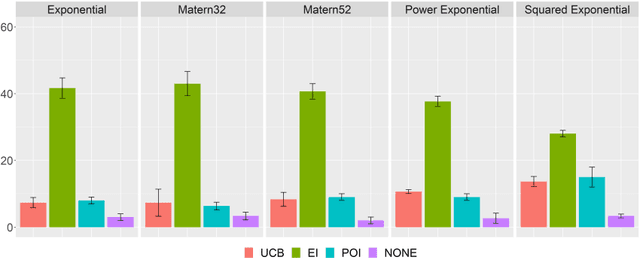
Modelling human function learning has been the subject of in-tense research in cognitive sciences. The topic is relevant in black-box optimization where information about the objective and/or constraints is not available and must be learned through function evaluations. In this paper we focus on the relation between the behaviour of humans searching for the maximum and the probabilistic model used in Bayesian Optimization. As surrogate models of the unknown function both Gaussian Processes and Random Forest have been considered: the Bayesian learning paradigm is central in the development of active learning approaches balancing exploration/exploitation in uncertain conditions towards effective generalization in large decision spaces. In this paper we analyse experimentally how Bayesian Optimization compares to humans searching for the maximum of an unknown 2D function. A set of controlled experiments with 60 subjects, using both surrogate models, confirm that Bayesian Optimization provides a general model to represent individual patterns of active learning in humans

Composition of kernel and acquisition functions for High Dimensional Bayesian Optimization

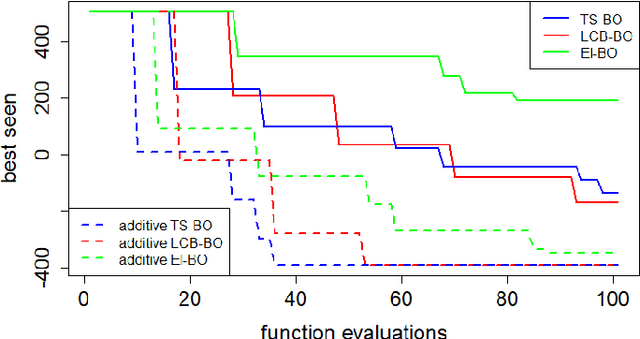
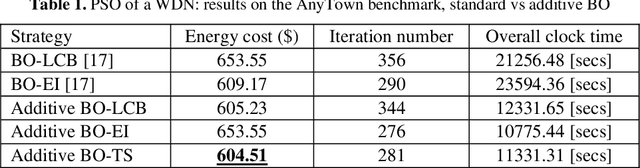
Bayesian Optimization has become the reference method for the global optimization of black box, expensive and possibly noisy functions. Bayesian Op-timization learns a probabilistic model about the objective function, usually a Gaussian Process, and builds, depending on its mean and variance, an acquisition function whose optimizer yields the new evaluation point, leading to update the probabilistic surrogate model. Despite its sample efficiency, Bayesian Optimiza-tion does not scale well with the dimensions of the problem. The optimization of the acquisition function has received less attention because its computational cost is usually considered negligible compared to that of the evaluation of the objec-tive function. Its efficient optimization is often inhibited, particularly in high di-mensional problems, by multiple extrema. In this paper we leverage the addition-ality of the objective function into mapping both the kernel and the acquisition function of the Bayesian Optimization in lower dimensional subspaces. This ap-proach makes more efficient the learning/updating of the probabilistic surrogate model and allows an efficient optimization of the acquisition function. Experi-mental results are presented for real-life application, that is the control of pumps in urban water distribution systems.

Safe global optimization of expensive noisy black-box functions in the $δ$-Lipschitz framework

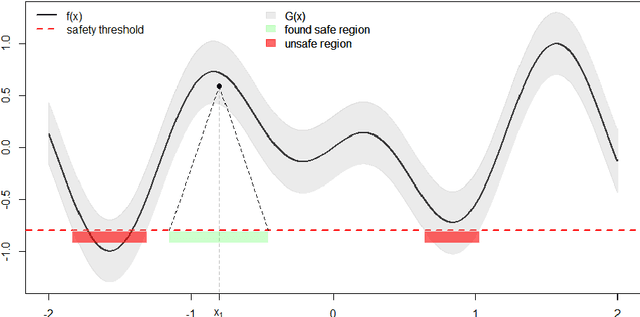
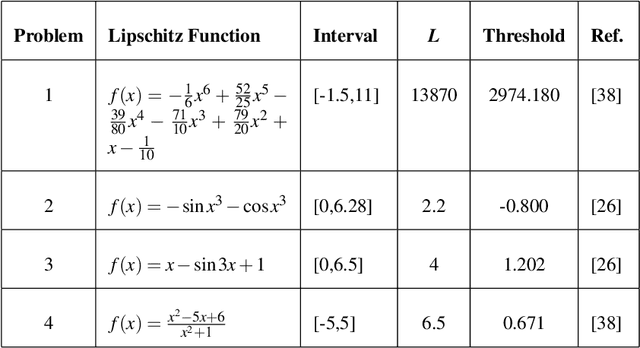
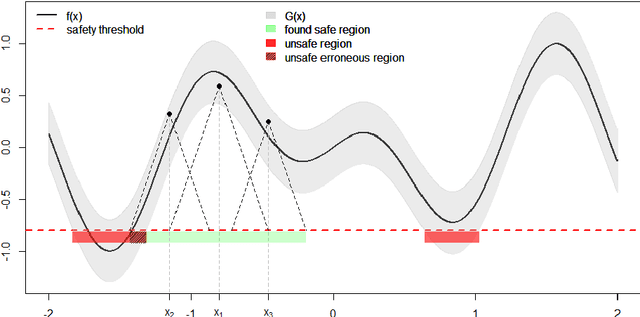
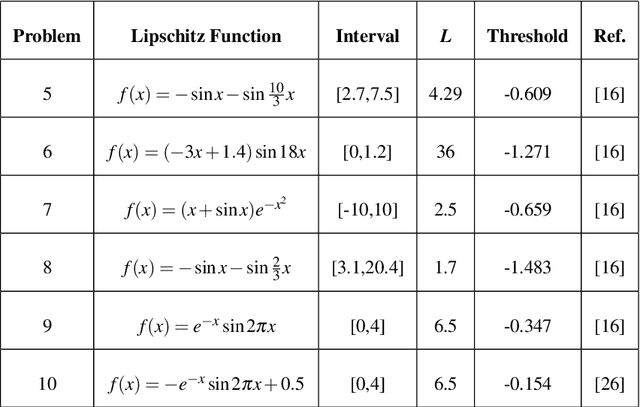
In this paper, the problem of safe global maximization (it should not be confused with robust optimization) of expensive noisy black-box functions satisfying the Lipschitz condition is considered. The notion "safe" means that the objective function $f(x)$ during optimization should not violate a "safety" threshold, for instance, a certain a priori given value $h$ in a maximization problem. Thus, any new function evaluation must be performed at "safe points" only, namely, at points $y$ for which it is known that the objective function $f(y) > h$. The main difficulty here consists in the fact that the used optimization algorithm should ensure that the safety constraint will be satisfied at a point $y$ before evaluation of $f(y)$ will be executed. Thus, it is required both to determine the safe region $\Omega$ within the search domain~$D$ and to find the global maximum within $\Omega$. An additional difficulty consists in the fact that these problems should be solved in the presence of the noise. This paper starts with a theoretical study of the problem and it is shown that even though the objective function $f(x)$ satisfies the Lipschitz condition, traditional Lipschitz minorants and majorants cannot be used due to the presence of the noise. Then, a $\delta$-Lipschitz framework and two algorithms using it are proposed to solve the safe global maximization problem. The first method determines the safe area within the search domain and the second one executes the global maximization over the found safe region. For both methods a number of theoretical results related to their functioning and convergence is established. Finally, numerical experiments confirming the reliability of the proposed procedures are performed.