A Bayesian approach for prompt optimization in pre-trained language models

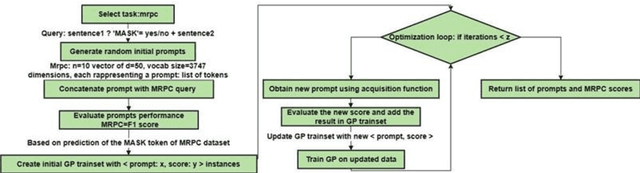
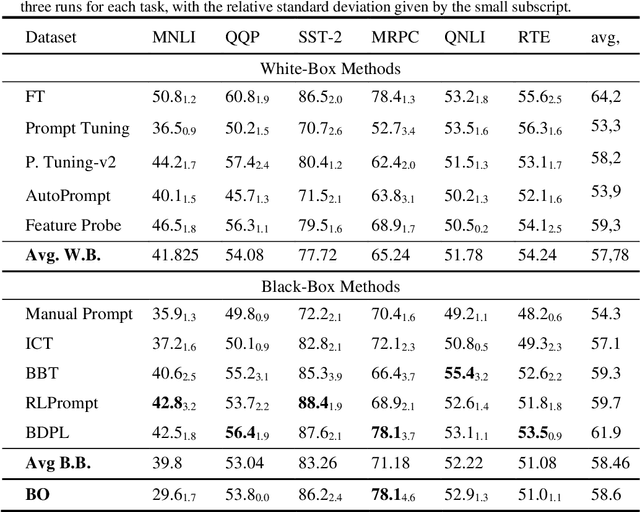
A prompt is a sequence of symbol or tokens, selected from a vocabulary according to some rule, which is prepended/concatenated to a textual query. A key problem is how to select the sequence of tokens: in this paper we formulate it as a combinatorial optimization problem. The high dimensionality of the token space com-pounded by the length of the prompt sequence requires a very efficient solution. In this paper we propose a Bayesian optimization method, executed in a continuous em-bedding of the combinatorial space. In this paper we focus on hard prompt tuning (HPT) which directly searches for discrete tokens to be added to the text input with-out requiring access to the large language model (LLM) and can be used also when LLM is available only as a black-box. This is critically important if LLMs are made available in the Model as a Service (MaaS) manner as in GPT-4. The current manu-script is focused on the optimization of discrete prompts for classification tasks. The discrete prompts give rise to difficult combinatorial optimization problem which easily become intractable given the dimension of the token space in realistic applications. The optimization method considered in this paper is Bayesian optimization (BO) which has become the dominant approach in black-box optimization for its sample efficiency along with its modular structure and versatility. In this paper we use BoTorch, a library for Bayesian optimization research built on top of pyTorch. Albeit preliminary and obtained using a 'vanilla' version of BO, the experiments on RoB-ERTa on six benchmarks, show a good performance across a variety of tasks and enable an analysis of the tradeoff between size of the search space, accuracy and wall clock time.

Modelling Human Active Search in Optimizing Black-box Functions

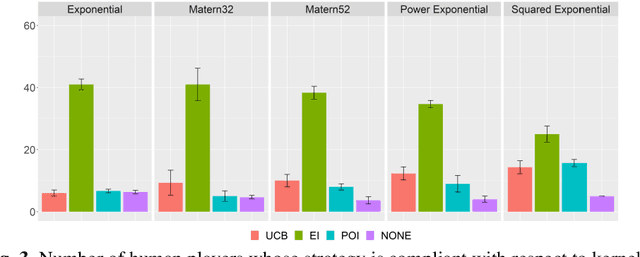
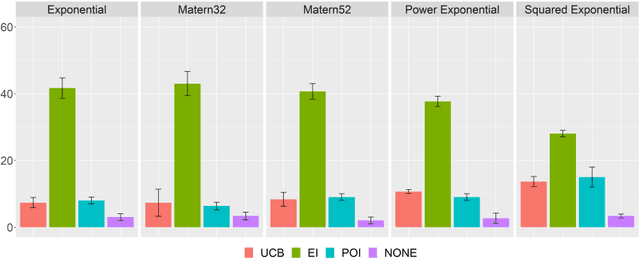
Modelling human function learning has been the subject of in-tense research in cognitive sciences. The topic is relevant in black-box optimization where information about the objective and/or constraints is not available and must be learned through function evaluations. In this paper we focus on the relation between the behaviour of humans searching for the maximum and the probabilistic model used in Bayesian Optimization. As surrogate models of the unknown function both Gaussian Processes and Random Forest have been considered: the Bayesian learning paradigm is central in the development of active learning approaches balancing exploration/exploitation in uncertain conditions towards effective generalization in large decision spaces. In this paper we analyse experimentally how Bayesian Optimization compares to humans searching for the maximum of an unknown 2D function. A set of controlled experiments with 60 subjects, using both surrogate models, confirm that Bayesian Optimization provides a general model to represent individual patterns of active learning in humans

Composition of kernel and acquisition functions for High Dimensional Bayesian Optimization

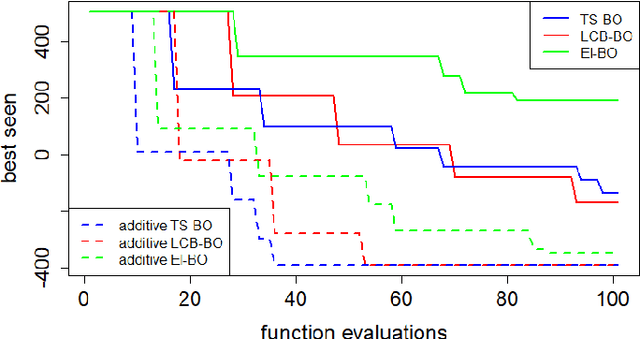
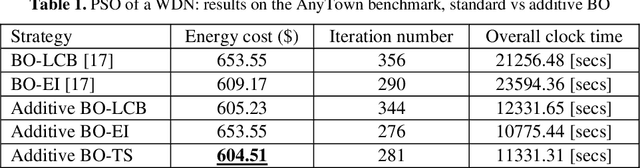
Bayesian Optimization has become the reference method for the global optimization of black box, expensive and possibly noisy functions. Bayesian Op-timization learns a probabilistic model about the objective function, usually a Gaussian Process, and builds, depending on its mean and variance, an acquisition function whose optimizer yields the new evaluation point, leading to update the probabilistic surrogate model. Despite its sample efficiency, Bayesian Optimiza-tion does not scale well with the dimensions of the problem. The optimization of the acquisition function has received less attention because its computational cost is usually considered negligible compared to that of the evaluation of the objec-tive function. Its efficient optimization is often inhibited, particularly in high di-mensional problems, by multiple extrema. In this paper we leverage the addition-ality of the objective function into mapping both the kernel and the acquisition function of the Bayesian Optimization in lower dimensional subspaces. This ap-proach makes more efficient the learning/updating of the probabilistic surrogate model and allows an efficient optimization of the acquisition function. Experi-mental results are presented for real-life application, that is the control of pumps in urban water distribution systems.