Graph data augmentation with Gromow-Wasserstein Barycenters

Graphs are ubiquitous in various fields, and deep learning methods have been successful applied in graph classification tasks. However, building large and diverse graph datasets for training can be expensive. While augmentation techniques exist for structured data like images or numerical data, the augmentation of graph data remains challenging. This is primarily due to the complex and non-Euclidean nature of graph data. In this paper, it has been proposed a novel augmentation strategy for graphs that operates in a non-Euclidean space. This approach leverages graphon estimation, which models the generative mechanism of networks sequences. Computational results demonstrate the effectiveness of the proposed augmentation framework in improving the performance of graph classification models. Additionally, using a non-Euclidean distance, specifically the Gromow-Wasserstein distance, results in better approximations of the graphon. This framework also provides a means to validate different graphon estimation approaches, particularly in real-world scenarios where the true graphon is unknown.

A Bayesian approach for prompt optimization in pre-trained language models

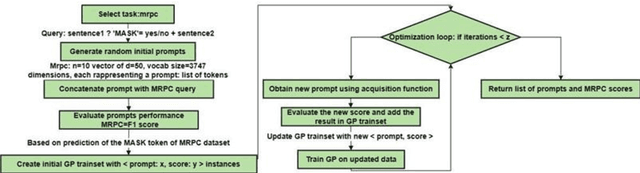
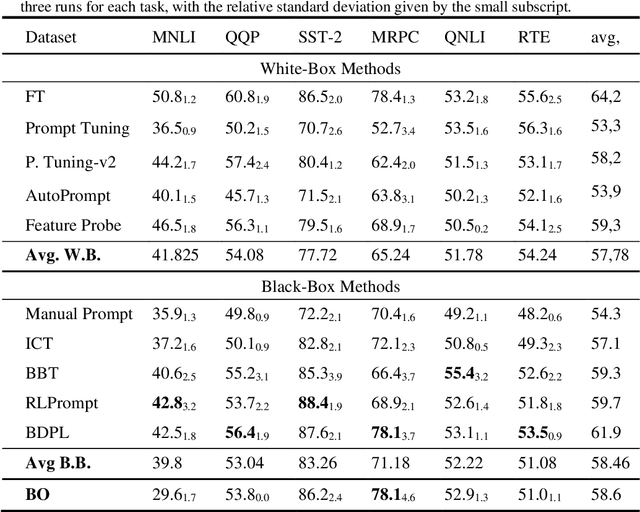
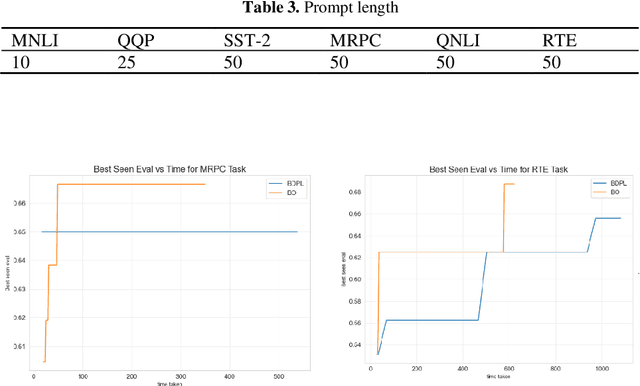
A prompt is a sequence of symbol or tokens, selected from a vocabulary according to some rule, which is prepended/concatenated to a textual query. A key problem is how to select the sequence of tokens: in this paper we formulate it as a combinatorial optimization problem. The high dimensionality of the token space com-pounded by the length of the prompt sequence requires a very efficient solution. In this paper we propose a Bayesian optimization method, executed in a continuous em-bedding of the combinatorial space. In this paper we focus on hard prompt tuning (HPT) which directly searches for discrete tokens to be added to the text input with-out requiring access to the large language model (LLM) and can be used also when LLM is available only as a black-box. This is critically important if LLMs are made available in the Model as a Service (MaaS) manner as in GPT-4. The current manu-script is focused on the optimization of discrete prompts for classification tasks. The discrete prompts give rise to difficult combinatorial optimization problem which easily become intractable given the dimension of the token space in realistic applications. The optimization method considered in this paper is Bayesian optimization (BO) which has become the dominant approach in black-box optimization for its sample efficiency along with its modular structure and versatility. In this paper we use BoTorch, a library for Bayesian optimization research built on top of pyTorch. Albeit preliminary and obtained using a 'vanilla' version of BO, the experiments on RoB-ERTa on six benchmarks, show a good performance across a variety of tasks and enable an analysis of the tradeoff between size of the search space, accuracy and wall clock time.

Gaussian Process regression over discrete probability measures: on the non-stationarity relation between Euclidean and Wasserstein Squared Exponential Kernels

Gaussian Process regression is a kernel method successfully adopted in many real-life applications. Recently, there is a growing interest on extending this method to non-Euclidean input spaces, like the one considered in this paper, consisting of probability measures. Although a Positive Definite kernel can be defined by using a suitable distance -- the Wasserstein distance -- the common procedure for learning the Gaussian Process model can fail due to numerical issues, arising earlier and more frequently than in the case of an Euclidean input space and, as demonstrated in this paper, that cannot be avoided by adding artificial noise (nugget effect) as usually done. This paper uncovers the main reason of these issues, that is a non-stationarity relationship between the Wasserstein-based squared exponential kernel and its Euclidean-based counterpart. As a relevant result, the Gaussian Process model is learned by assuming the input space as Euclidean and then an algebraic transformation, based on the uncovered relation, is used to transform it into a non-stationary and Wasserstein-based Gaussian Process model over probability measures. This algebraic transformation is simpler than log-exp maps used in the case of data belonging to Riemannian manifolds and recently extended to consider the pseudo-Riemannian structure of an input space equipped with the Wasserstein distance.

BORA: Bayesian Optimization for Resource Allocation

Optimal resource allocation is gaining a renewed interest due its relevance as a core problem in managing, over time, cloud and high-performance computing facilities. Semi-Bandit Feedback (SBF) is the reference method for efficiently solving this problem. In this paper we propose (i) an extension of the optimal resource allocation to a more general class of problems, specifically with resources availability changing over time, and (ii) Bayesian Optimization as a more efficient alternative to SBF. Three algorithms for Bayesian Optimization for Resource Allocation, namely BORA, are presented, working on allocation decisions represented as numerical vectors or distributions. The second option required to consider the Wasserstein distance as a more suitable metric to use into one of the BORA algorithms. Results on (i) the original SBF case study proposed in the literature, and (ii) a real-life application (i.e., the optimization of multi-channel marketing) empirically prove that BORA is a more efficient and effective learning-and-optimization framework than SBF.

Fair and Green Hyperparameter Optimization via Multi-objective and Multiple Information Source Bayesian Optimization

There is a consensus that focusing only on accuracy in searching for optimal machine learning models amplifies biases contained in the data, leading to unfair predictions and decision supports. Recently, multi-objective hyperparameter optimization has been proposed to search for machine learning models which offer equally Pareto-efficient trade-offs between accuracy and fairness. Although these approaches proved to be more versatile than fairness-aware machine learning algorithms -- which optimize accuracy constrained to some threshold on fairness -- they could drastically increase the energy consumption in the case of large datasets. In this paper we propose FanG-HPO, a Fair and Green Hyperparameter Optimization (HPO) approach based on both multi-objective and multiple information source Bayesian optimization. FanG-HPO uses subsets of the large dataset (aka information sources) to obtain cheap approximations of both accuracy and fairness, and multi-objective Bayesian Optimization to efficiently identify Pareto-efficient machine learning models. Experiments consider two benchmark (fairness) datasets and two machine learning algorithms (XGBoost and Multi-Layer Perceptron), and provide an assessment of FanG-HPO against both fairness-aware machine learning algorithms and hyperparameter optimization via a multi-objective single-source optimization algorithm in BoTorch, a state-of-the-art platform for Bayesian Optimization.

Gamifying optimization: a Wasserstein distance-based analysis of human search

The main objective of this paper is to outline a theoretical framework to characterise humans' decision-making strategies under uncertainty, in particular active learning in a black-box optimization task and trading-off between information gathering (exploration) and reward seeking (exploitation). Humans' decisions making according to these two objectives can be modelled in terms of Pareto rationality. If a decision set contains a Pareto efficient strategy, a rational decision maker should always select the dominant strategy over its dominated alternatives. A distance from the Pareto frontier determines whether a choice is Pareto rational. To collect data about humans' strategies we have used a gaming application that shows the game field, with previous decisions and observations, as well as the score obtained. The key element in this paper is the representation of behavioural patterns of human learners as a discrete probability distribution. This maps the problem of the characterization of humans' behaviour into a space whose elements are probability distributions structured by a distance between histograms, namely the Wasserstein distance (WST). The distributional analysis gives new insights about human search strategies and their deviations from Pareto rationality. Since the uncertainty is one of the two objectives defining the Pareto frontier, the analysis has been performed for three different uncertainty quantification measures to identify which better explains the Pareto compliant behavioural patterns. Beside the analysis of individual patterns WST has also enabled a global analysis computing the barycenters and WST k-means clustering. A further analysis has been performed by a decision tree to relate non-Paretian behaviour, characterized by exasperated exploitation, to the dynamics of the evolution of the reward seeking process.

Multi-Task Learning on Networks

The multi-task learning (MTL) paradigm can be traced back to an early paper of Caruana (1997) in which it was argued that data from multiple tasks can be used with the aim to obtain a better performance over learning each task independently. A solution of MTL with conflicting objectives requires modelling the trade-off among them which is generally beyond what a straight linear combination can achieve. A theoretically principled and computationally effective strategy is finding solutions which are not dominated by others as it is addressed in the Pareto analysis. Multi-objective optimization problems arising in the multi-task learning context have specific features and require adhoc methods. The analysis of these features and the proposal of a new computational approach represent the focus of this work. Multi-objective evolutionary algorithms (MOEAs) can easily include the concept of dominance and therefore the Pareto analysis. The major drawback of MOEAs is a low sample efficiency with respect to function evaluations. The key reason for this drawback is that most of the evolutionary approaches do not use models for approximating the objective function. Bayesian Optimization takes a radically different approach based on a surrogate model, such as a Gaussian Process. In this thesis the solutions in the Input Space are represented as probability distributions encapsulating the knowledge contained in the function evaluations. In this space of probability distributions, endowed with the metric given by the Wasserstein distance, a new algorithm MOEA/WST can be designed in which the model is not directly on the objective function but in an intermediate Information Space where the objects from the input space are mapped into histograms. Computational results show that the sample efficiency and the quality of the Pareto set provided by MOEA/WST are significantly better than in the standard MOEA.

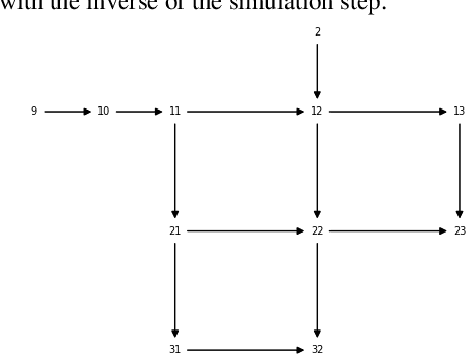
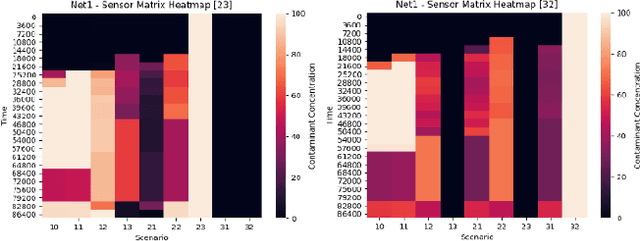
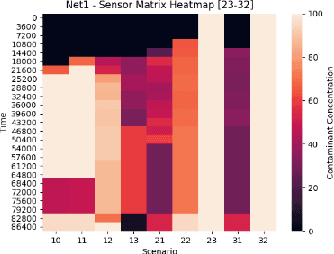
Risk Aware Optimization of Water Sensor Placement

Optimal sensor placement (SP) usually minimizes an impact measure, such as the amount of contaminated water or the number of inhabitants affected before detection. The common choice is to minimize the minimum detection time (MDT) averaged over a set of contamination events, with contaminant injected at a different location. Given a SP, propagation is simulated through a hydraulic software model of the network to obtain spatio-temporal concentrations and the average MDT. Searching for an optimal SP is NP-hard: even for mid-size networks, efficient search methods are required, among which evolutionary approaches are often used. A bi-objective formalization is proposed: minimizing the average MDT and its standard deviation, that is the risk to detect some contamination event too late than the average MDT. We propose a data structure (sort of spatio-temporal heatmap) collecting simulation outcomes for every SP and particularly suitable for evolutionary optimization. Indeed, the proposed data structure enabled a convergence analysis of a population-based algorithm, leading to the identification of indicators for detecting problem-specific converge issues which could be generalized to other similar problems. We used Pymoo, a recent Python framework flexible enough to incorporate our problem specific termination criterion. Results on a benchmark and a real-world network are presented.

Uncertainty quantification and exploration-exploitation trade-off in humans

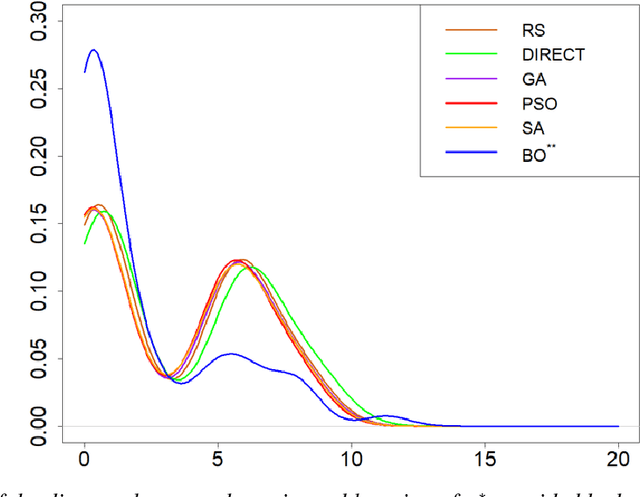
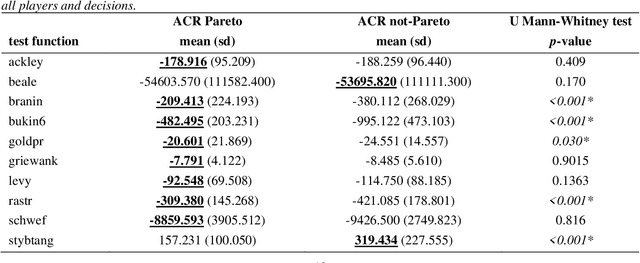
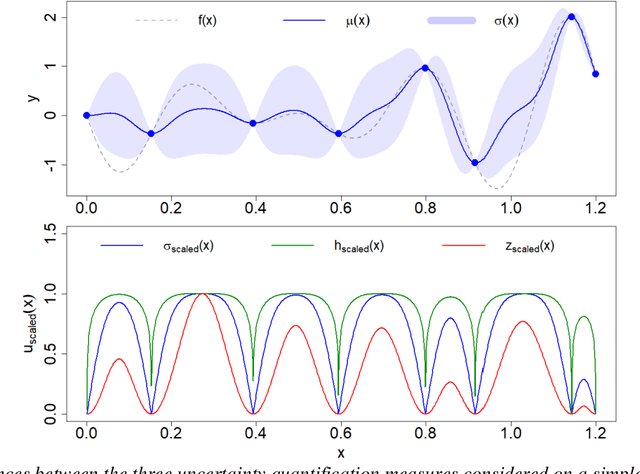
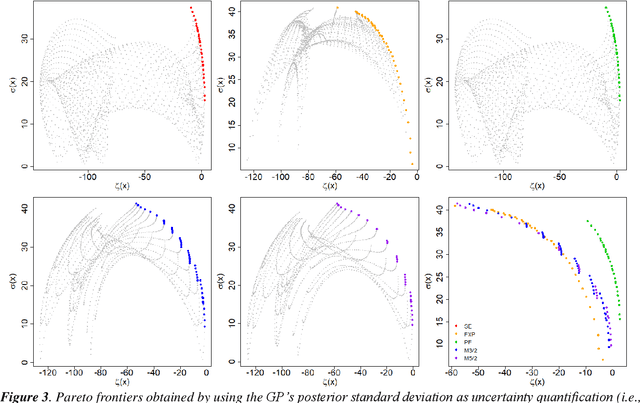
The main objective of this paper is to outline a theoretical framework to analyse how humans' decision-making strategies under uncertainty manage the trade-off between information gathering (exploration) and reward seeking (exploitation). A key observation, motivating this line of research, is the awareness that human learners are amazingly fast and effective at adapting to unfamiliar environments and incorporating upcoming knowledge: this is an intriguing behaviour for cognitive sciences as well as an important challenge for Machine Learning. The target problem considered is active learning in a black-box optimization task and more specifically how the exploration/exploitation dilemma can be modelled within Gaussian Process based Bayesian Optimization framework, which is in turn based on uncertainty quantification. The main contribution is to analyse humans' decisions with respect to Pareto rationality where the two objectives are improvement expected and uncertainty quantification. According to this Pareto rationality model, if a decision set contains a Pareto efficient (dominant) strategy, a rational decision maker should always select the dominant strategy over its dominated alternatives. The distance from the Pareto frontier determines whether a choice is (Pareto) rational (i.e., lays on the frontier) or is associated to "exasperate" exploration. However, since the uncertainty is one of the two objectives defining the Pareto frontier, we have investigated three different uncertainty quantification measures and selected the one resulting more compliant with the Pareto rationality model proposed. The key result is an analytical framework to characterize how deviations from "rationality" depend on uncertainty quantifications and the evolution of the reward seeking process.

Modelling Human Active Search in Optimizing Black-box Functions

Modelling human function learning has been the subject of in-tense research in cognitive sciences. The topic is relevant in black-box optimization where information about the objective and/or constraints is not available and must be learned through function evaluations. In this paper we focus on the relation between the behaviour of humans searching for the maximum and the probabilistic model used in Bayesian Optimization. As surrogate models of the unknown function both Gaussian Processes and Random Forest have been considered: the Bayesian learning paradigm is central in the development of active learning approaches balancing exploration/exploitation in uncertain conditions towards effective generalization in large decision spaces. In this paper we analyse experimentally how Bayesian Optimization compares to humans searching for the maximum of an unknown 2D function. A set of controlled experiments with 60 subjects, using both surrogate models, confirm that Bayesian Optimization provides a general model to represent individual patterns of active learning in humans