Uncertainty quantification and exploration-exploitation trade-off in humans
Paper and Code
Feb 05, 2021
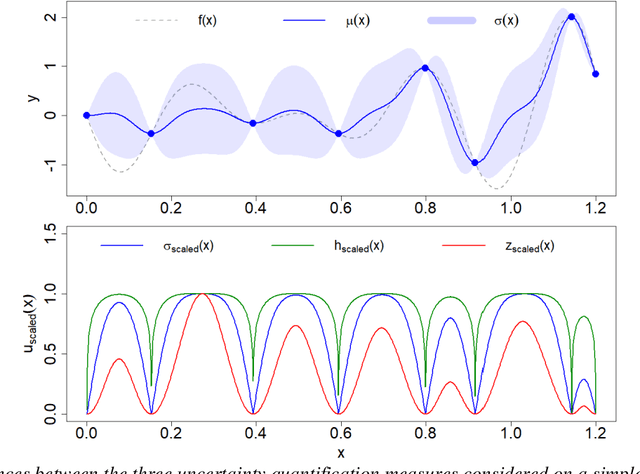
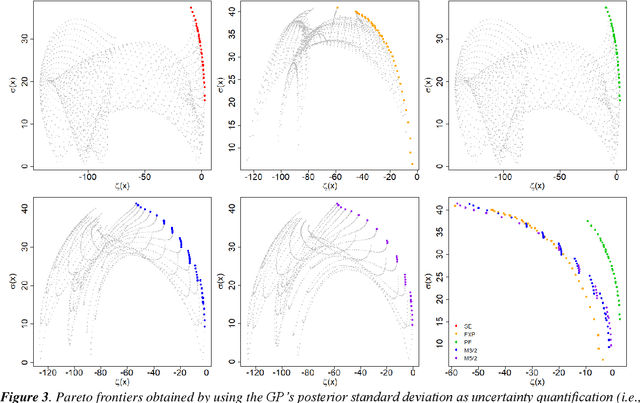
The main objective of this paper is to outline a theoretical framework to analyse how humans' decision-making strategies under uncertainty manage the trade-off between information gathering (exploration) and reward seeking (exploitation). A key observation, motivating this line of research, is the awareness that human learners are amazingly fast and effective at adapting to unfamiliar environments and incorporating upcoming knowledge: this is an intriguing behaviour for cognitive sciences as well as an important challenge for Machine Learning. The target problem considered is active learning in a black-box optimization task and more specifically how the exploration/exploitation dilemma can be modelled within Gaussian Process based Bayesian Optimization framework, which is in turn based on uncertainty quantification. The main contribution is to analyse humans' decisions with respect to Pareto rationality where the two objectives are improvement expected and uncertainty quantification. According to this Pareto rationality model, if a decision set contains a Pareto efficient (dominant) strategy, a rational decision maker should always select the dominant strategy over its dominated alternatives. The distance from the Pareto frontier determines whether a choice is (Pareto) rational (i.e., lays on the frontier) or is associated to "exasperate" exploration. However, since the uncertainty is one of the two objectives defining the Pareto frontier, we have investigated three different uncertainty quantification measures and selected the one resulting more compliant with the Pareto rationality model proposed. The key result is an analytical framework to characterize how deviations from "rationality" depend on uncertainty quantifications and the evolution of the reward seeking process.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge