A Bayesian approach for prompt optimization in pre-trained language models

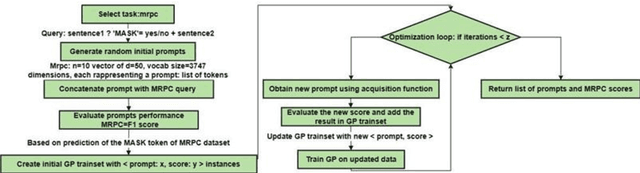
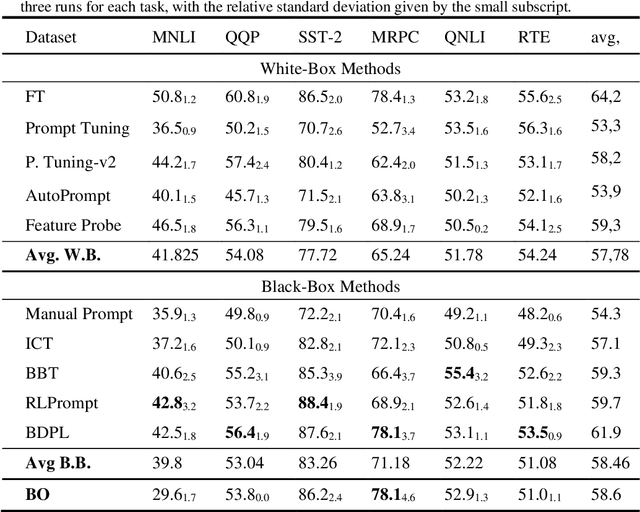
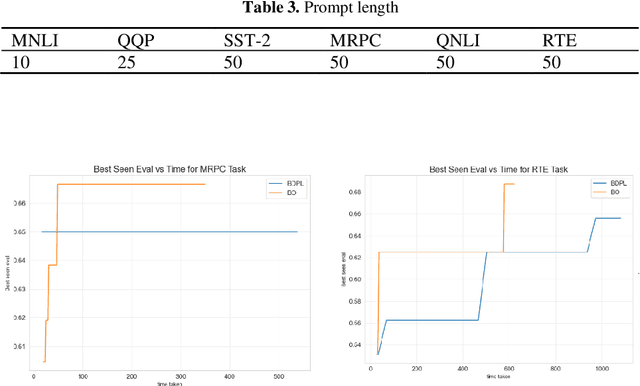
A prompt is a sequence of symbol or tokens, selected from a vocabulary according to some rule, which is prepended/concatenated to a textual query. A key problem is how to select the sequence of tokens: in this paper we formulate it as a combinatorial optimization problem. The high dimensionality of the token space com-pounded by the length of the prompt sequence requires a very efficient solution. In this paper we propose a Bayesian optimization method, executed in a continuous em-bedding of the combinatorial space. In this paper we focus on hard prompt tuning (HPT) which directly searches for discrete tokens to be added to the text input with-out requiring access to the large language model (LLM) and can be used also when LLM is available only as a black-box. This is critically important if LLMs are made available in the Model as a Service (MaaS) manner as in GPT-4. The current manu-script is focused on the optimization of discrete prompts for classification tasks. The discrete prompts give rise to difficult combinatorial optimization problem which easily become intractable given the dimension of the token space in realistic applications. The optimization method considered in this paper is Bayesian optimization (BO) which has become the dominant approach in black-box optimization for its sample efficiency along with its modular structure and versatility. In this paper we use BoTorch, a library for Bayesian optimization research built on top of pyTorch. Albeit preliminary and obtained using a 'vanilla' version of BO, the experiments on RoB-ERTa on six benchmarks, show a good performance across a variety of tasks and enable an analysis of the tradeoff between size of the search space, accuracy and wall clock time.

Mastering the exploration-exploitation trade-off in Bayesian Optimization

Gaussian Process based Bayesian Optimization is a well-known sample efficient sequential strategy for globally optimizing black-box, expensive, and multi-extremal functions. The role of the Gaussian Process is to provide a probabilistic approximation of the unknown function, depending on the sequentially collected observations, while an acquisition function drives the choice of the next solution to evaluate, balancing between exploration and exploitation, depending on the current Gaussian Process model. Despite the huge effort of the scientific community in defining effective exploration-exploitation mechanisms, we are still far away from the master acquisition function. This paper merges the most relevant results and insights from both algorithmic and human search strategies to propose a novel acquisition function, mastering the trade-off between explorative and exploitative choices, adaptively. We compare the proposed acquisition function on a number of test functions and against different state-of-the-art ones, which are instead based on prefixed or random scheduling between exploration and exploitation. A Pareto analysis is performed with respect to two (antagonistic) goals: convergence to the optimum and exploration capability. Results empirically prove that the proposed acquisition function is almost always Pareto optimal and also the most balanced trade-off between the two goals.

Gaussian Process regression over discrete probability measures: on the non-stationarity relation between Euclidean and Wasserstein Squared Exponential Kernels

Gaussian Process regression is a kernel method successfully adopted in many real-life applications. Recently, there is a growing interest on extending this method to non-Euclidean input spaces, like the one considered in this paper, consisting of probability measures. Although a Positive Definite kernel can be defined by using a suitable distance -- the Wasserstein distance -- the common procedure for learning the Gaussian Process model can fail due to numerical issues, arising earlier and more frequently than in the case of an Euclidean input space and, as demonstrated in this paper, that cannot be avoided by adding artificial noise (nugget effect) as usually done. This paper uncovers the main reason of these issues, that is a non-stationarity relationship between the Wasserstein-based squared exponential kernel and its Euclidean-based counterpart. As a relevant result, the Gaussian Process model is learned by assuming the input space as Euclidean and then an algebraic transformation, based on the uncovered relation, is used to transform it into a non-stationary and Wasserstein-based Gaussian Process model over probability measures. This algebraic transformation is simpler than log-exp maps used in the case of data belonging to Riemannian manifolds and recently extended to consider the pseudo-Riemannian structure of an input space equipped with the Wasserstein distance.

BORA: Bayesian Optimization for Resource Allocation

Optimal resource allocation is gaining a renewed interest due its relevance as a core problem in managing, over time, cloud and high-performance computing facilities. Semi-Bandit Feedback (SBF) is the reference method for efficiently solving this problem. In this paper we propose (i) an extension of the optimal resource allocation to a more general class of problems, specifically with resources availability changing over time, and (ii) Bayesian Optimization as a more efficient alternative to SBF. Three algorithms for Bayesian Optimization for Resource Allocation, namely BORA, are presented, working on allocation decisions represented as numerical vectors or distributions. The second option required to consider the Wasserstein distance as a more suitable metric to use into one of the BORA algorithms. Results on (i) the original SBF case study proposed in the literature, and (ii) a real-life application (i.e., the optimization of multi-channel marketing) empirically prove that BORA is a more efficient and effective learning-and-optimization framework than SBF.

Fair and Green Hyperparameter Optimization via Multi-objective and Multiple Information Source Bayesian Optimization

There is a consensus that focusing only on accuracy in searching for optimal machine learning models amplifies biases contained in the data, leading to unfair predictions and decision supports. Recently, multi-objective hyperparameter optimization has been proposed to search for machine learning models which offer equally Pareto-efficient trade-offs between accuracy and fairness. Although these approaches proved to be more versatile than fairness-aware machine learning algorithms -- which optimize accuracy constrained to some threshold on fairness -- they could drastically increase the energy consumption in the case of large datasets. In this paper we propose FanG-HPO, a Fair and Green Hyperparameter Optimization (HPO) approach based on both multi-objective and multiple information source Bayesian optimization. FanG-HPO uses subsets of the large dataset (aka information sources) to obtain cheap approximations of both accuracy and fairness, and multi-objective Bayesian Optimization to efficiently identify Pareto-efficient machine learning models. Experiments consider two benchmark (fairness) datasets and two machine learning algorithms (XGBoost and Multi-Layer Perceptron), and provide an assessment of FanG-HPO against both fairness-aware machine learning algorithms and hyperparameter optimization via a multi-objective single-source optimization algorithm in BoTorch, a state-of-the-art platform for Bayesian Optimization.

Gamifying optimization: a Wasserstein distance-based analysis of human search

The main objective of this paper is to outline a theoretical framework to characterise humans' decision-making strategies under uncertainty, in particular active learning in a black-box optimization task and trading-off between information gathering (exploration) and reward seeking (exploitation). Humans' decisions making according to these two objectives can be modelled in terms of Pareto rationality. If a decision set contains a Pareto efficient strategy, a rational decision maker should always select the dominant strategy over its dominated alternatives. A distance from the Pareto frontier determines whether a choice is Pareto rational. To collect data about humans' strategies we have used a gaming application that shows the game field, with previous decisions and observations, as well as the score obtained. The key element in this paper is the representation of behavioural patterns of human learners as a discrete probability distribution. This maps the problem of the characterization of humans' behaviour into a space whose elements are probability distributions structured by a distance between histograms, namely the Wasserstein distance (WST). The distributional analysis gives new insights about human search strategies and their deviations from Pareto rationality. Since the uncertainty is one of the two objectives defining the Pareto frontier, the analysis has been performed for three different uncertainty quantification measures to identify which better explains the Pareto compliant behavioural patterns. Beside the analysis of individual patterns WST has also enabled a global analysis computing the barycenters and WST k-means clustering. A further analysis has been performed by a decision tree to relate non-Paretian behaviour, characterized by exasperated exploitation, to the dynamics of the evolution of the reward seeking process.

Bayesian Optimization and Deep Learning forsteering wheel angle prediction

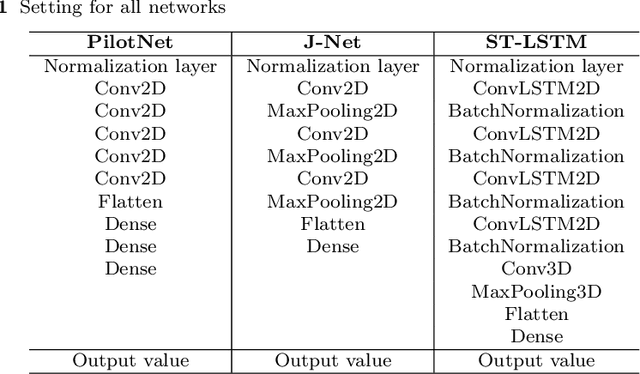
Automated driving systems (ADS) have undergone a significant improvement in the last years. ADS and more precisely self-driving cars technologies will change the way we perceive and know the world of transportation systems in terms of user experience, mode choices and business models. The emerging field of Deep Learning (DL) has been successfully applied for the development of innovative ADS solutions. However, the attempt to single out the best deep neural network architecture and tuning its hyperparameters are all expensive processes, both in terms of time and computational resources. In this work, Bayesian Optimization (BO) is used to optimize the hyperparameters of a Spatiotemporal-Long Short Term Memory (ST-LSTM) network with the aim to obtain an accurate model for the prediction of the steering angle in a ADS. BO was able to identify, within a limited number of trials, a model -- namely BOST-LSTM -- which resulted, on a public dataset, the most accurate when compared to classical end-to-end driving models.

Risk Aware Optimization of Water Sensor Placement

Optimal sensor placement (SP) usually minimizes an impact measure, such as the amount of contaminated water or the number of inhabitants affected before detection. The common choice is to minimize the minimum detection time (MDT) averaged over a set of contamination events, with contaminant injected at a different location. Given a SP, propagation is simulated through a hydraulic software model of the network to obtain spatio-temporal concentrations and the average MDT. Searching for an optimal SP is NP-hard: even for mid-size networks, efficient search methods are required, among which evolutionary approaches are often used. A bi-objective formalization is proposed: minimizing the average MDT and its standard deviation, that is the risk to detect some contamination event too late than the average MDT. We propose a data structure (sort of spatio-temporal heatmap) collecting simulation outcomes for every SP and particularly suitable for evolutionary optimization. Indeed, the proposed data structure enabled a convergence analysis of a population-based algorithm, leading to the identification of indicators for detecting problem-specific converge issues which could be generalized to other similar problems. We used Pymoo, a recent Python framework flexible enough to incorporate our problem specific termination criterion. Results on a benchmark and a real-world network are presented.

MISO-wiLDCosts: Multi Information Source Optimization with Location Dependent Costs

This paper addresses black-box optimization over multiple information sources whose both fidelity and query cost change over the search space, that is they are location dependent. The approach uses: (i) an Augmented Gaussian Process, recently proposed in multi-information source optimization as a single model of the objective function over search space and sources, and (ii) a Gaussian Process to model the location-dependent cost of each source. The former is used into a Confidence Bound based acquisition function to select the next source and location to query, while the latter is used to penalize the value of the acquisition depending on the expected query cost for any source-location pair. The proposed approach is evaluated on a set of Hyperparameters Optimization tasks, consisting of two Machine Learning classifiers and three datasets of different sizes.

Uncertainty quantification and exploration-exploitation trade-off in humans

The main objective of this paper is to outline a theoretical framework to analyse how humans' decision-making strategies under uncertainty manage the trade-off between information gathering (exploration) and reward seeking (exploitation). A key observation, motivating this line of research, is the awareness that human learners are amazingly fast and effective at adapting to unfamiliar environments and incorporating upcoming knowledge: this is an intriguing behaviour for cognitive sciences as well as an important challenge for Machine Learning. The target problem considered is active learning in a black-box optimization task and more specifically how the exploration/exploitation dilemma can be modelled within Gaussian Process based Bayesian Optimization framework, which is in turn based on uncertainty quantification. The main contribution is to analyse humans' decisions with respect to Pareto rationality where the two objectives are improvement expected and uncertainty quantification. According to this Pareto rationality model, if a decision set contains a Pareto efficient (dominant) strategy, a rational decision maker should always select the dominant strategy over its dominated alternatives. The distance from the Pareto frontier determines whether a choice is (Pareto) rational (i.e., lays on the frontier) or is associated to "exasperate" exploration. However, since the uncertainty is one of the two objectives defining the Pareto frontier, we have investigated three different uncertainty quantification measures and selected the one resulting more compliant with the Pareto rationality model proposed. The key result is an analytical framework to characterize how deviations from "rationality" depend on uncertainty quantifications and the evolution of the reward seeking process.