Composition of kernel and acquisition functions for High Dimensional Bayesian Optimization
Paper and Code
Mar 09, 2020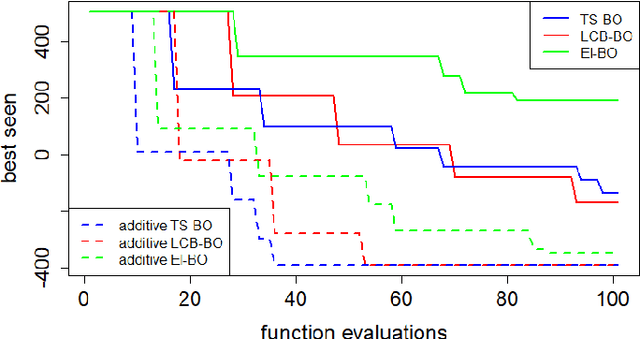
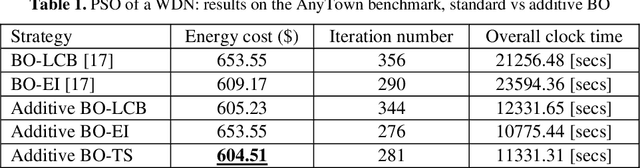
Bayesian Optimization has become the reference method for the global optimization of black box, expensive and possibly noisy functions. Bayesian Op-timization learns a probabilistic model about the objective function, usually a Gaussian Process, and builds, depending on its mean and variance, an acquisition function whose optimizer yields the new evaluation point, leading to update the probabilistic surrogate model. Despite its sample efficiency, Bayesian Optimiza-tion does not scale well with the dimensions of the problem. The optimization of the acquisition function has received less attention because its computational cost is usually considered negligible compared to that of the evaluation of the objec-tive function. Its efficient optimization is often inhibited, particularly in high di-mensional problems, by multiple extrema. In this paper we leverage the addition-ality of the objective function into mapping both the kernel and the acquisition function of the Bayesian Optimization in lower dimensional subspaces. This ap-proach makes more efficient the learning/updating of the probabilistic surrogate model and allows an efficient optimization of the acquisition function. Experi-mental results are presented for real-life application, that is the control of pumps in urban water distribution systems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge