Reshma Rastogi
nee. Khemchandani
GBSVR: Granular Ball Support Vector Regression
Mar 13, 2025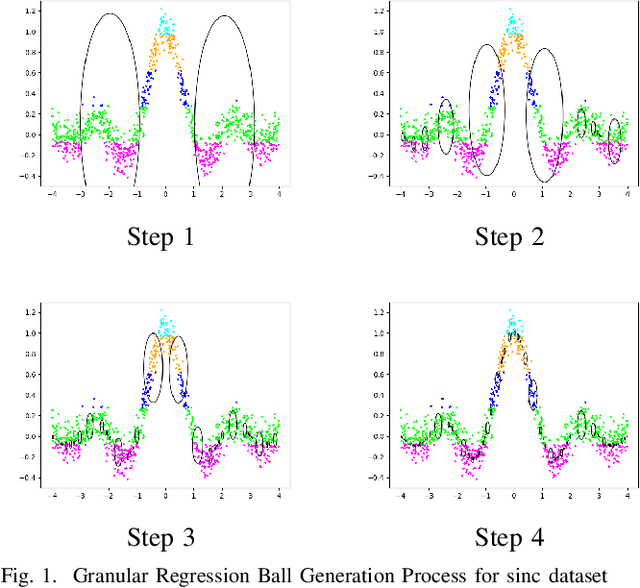

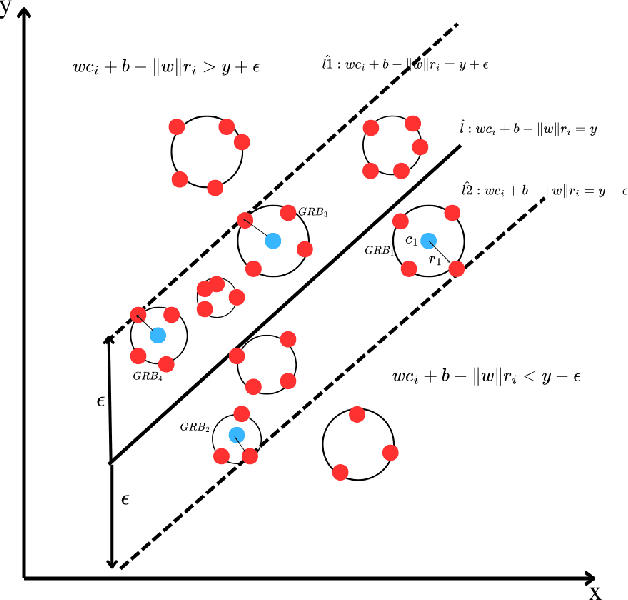
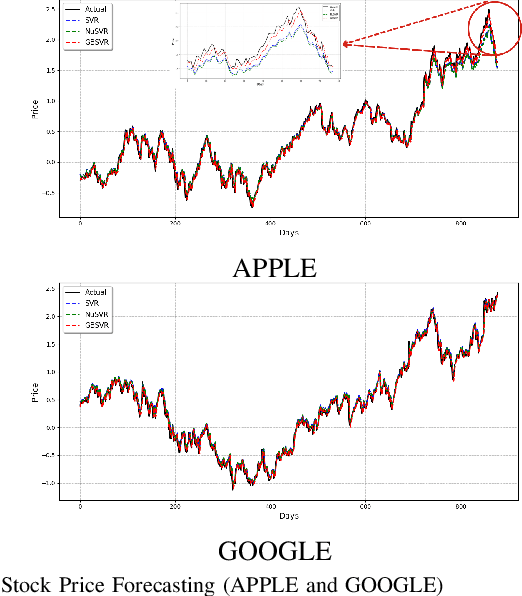
Abstract:Support Vector Regression (SVR) and its variants are widely used to handle regression tasks, however, since their solution involves solving an expensive quadratic programming problem, it limits its application, especially when dealing with large datasets. Additionally, SVR uses an epsilon-insensitive loss function which is sensitive to outliers and therefore can adversely affect its performance. We propose Granular Ball Support Vector Regression (GBSVR) to tackle problem of regression by using granular ball concept. These balls are useful in simplifying complex data spaces for machine learning tasks, however, to the best of our knowledge, they have not been sufficiently explored for regression problems. Granular balls group the data points into balls based on their proximity and reduce the computational cost in SVR by replacing the large number of data points with far fewer granular balls. This work also suggests a discretization method for continuous-valued attributes to facilitate the construction of granular balls. The effectiveness of the proposed approach is evaluated on several benchmark datasets and it outperforms existing state-of-the-art approaches
Efficient Learning of Pinball TWSVM using Privileged Information and its applications
Jul 14, 2021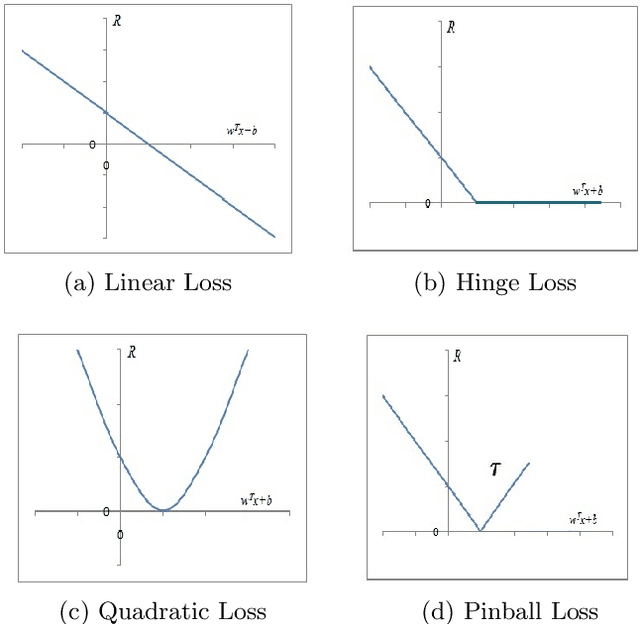
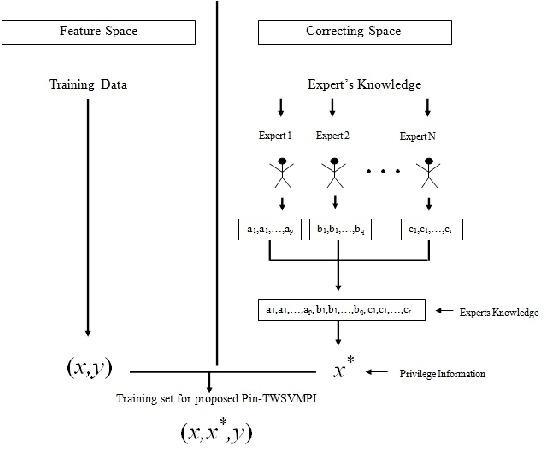
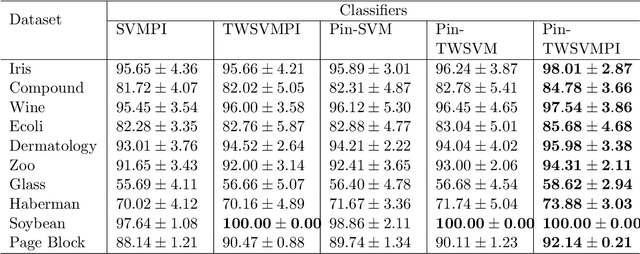
Abstract:In any learning framework, an expert knowledge always plays a crucial role. But, in the field of machine learning, the knowledge offered by an expert is rarely used. Moreover, machine learning algorithms (SVM based) generally use hinge loss function which is sensitive towards the noise. Thus, in order to get the advantage from an expert knowledge and to reduce the sensitivity towards the noise, in this paper, we propose privileged information based Twin Pinball Support Vector Machine classifier (Pin-TWSVMPI) where expert's knowledge is in the form of privileged information. The proposed Pin-TWSVMPI incorporates privileged information by using correcting function so as to obtain two nonparallel decision hyperplanes. Further, in order to make computations more efficient and fast, we use Sequential Minimal Optimization (SMO) technique for obtaining the classifier and have also shown its application for Pedestrian detection and Handwritten digit recognition. Further, for UCI datasets, we first implement a procedure which extracts privileged information from the features of the dataset which are then further utilized by Pin-TWSVMPI that leads to enhancement in classification accuracy with comparatively lesser computational time.
Improvement over Pinball Loss Support Vector Machine
Jun 02, 2021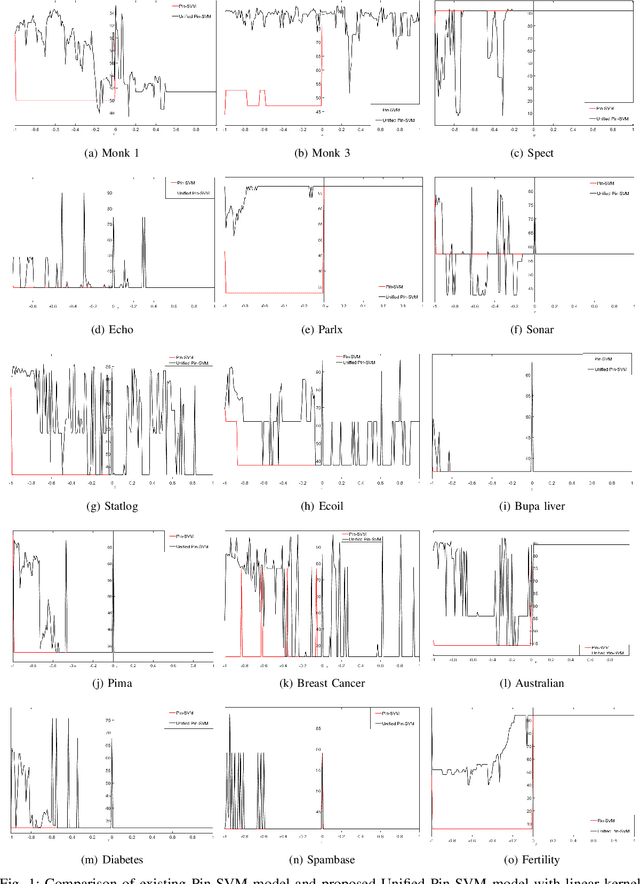
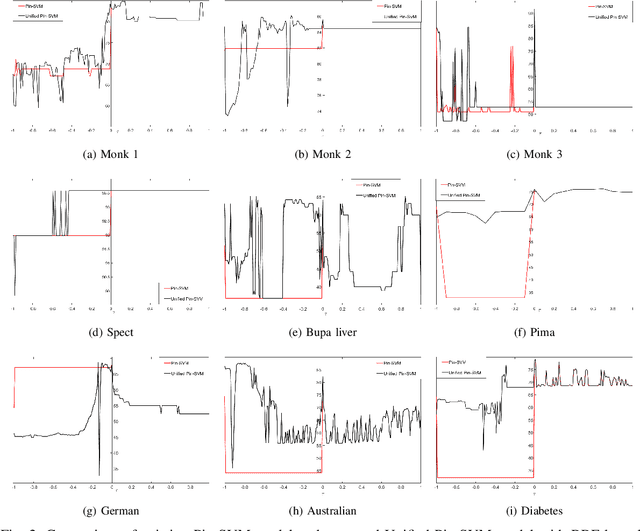
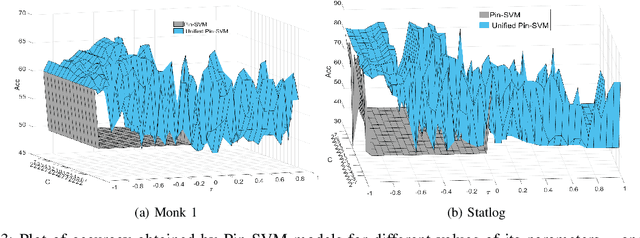
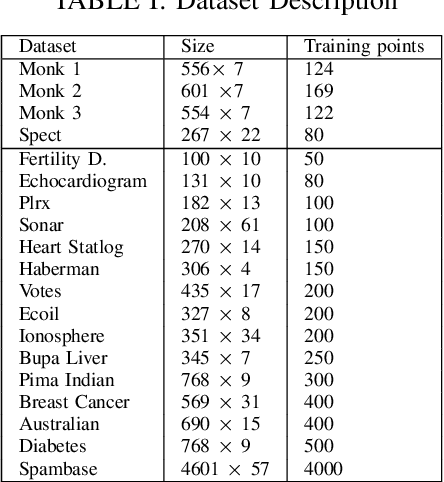
Abstract:Recently, there have been several papers that discuss the extension of the Pinball loss Support Vector Machine (Pin-SVM) model, originally proposed by Huang et al.,[1][2]. Pin-SVM classifier deals with the pinball loss function, which has been defined in terms of the parameter $\tau$. The parameter $\tau$ can take values in $[ -1,1]$. The existing Pin-SVM model requires to solve the same optimization problem for all values of $\tau$ in $[ -1,1]$. In this paper, we improve the existing Pin-SVM model for the binary classification task. At first, we note that there is major difficulty in Pin-SVM model (Huang et al. [1]) for $ -1 \leq \tau < 0$. Specifically, we show that the Pin-SVM model requires the solution of different optimization problem for $ -1 \leq \tau < 0$. We further propose a unified model termed as Unified Pin-SVM which results in a QPP valid for all $-1\leq \tau \leq 1$ and hence more convenient to use. The proposed Unified Pin-SVM model can obtain a significant improvement in accuracy over the existing Pin-SVM model which has also been empirically justified by extensive numerical experiments with real-world datasets.
A $ν$- support vector quantile regression model with automatic accuracy control
Oct 21, 2019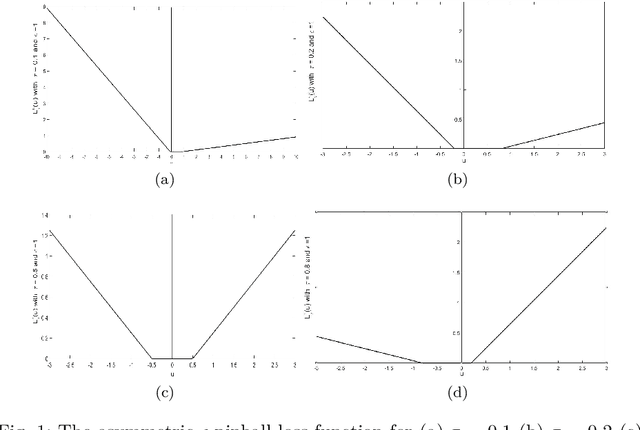
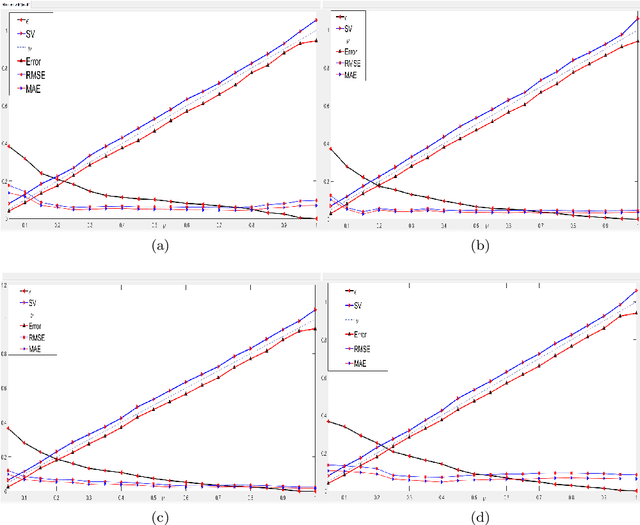
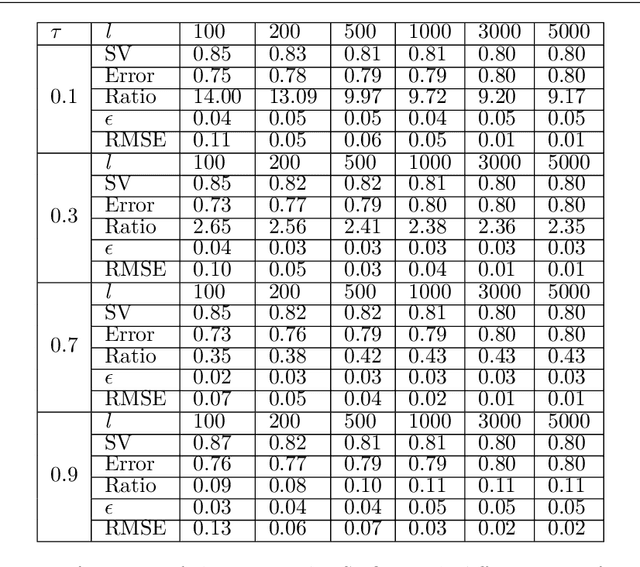
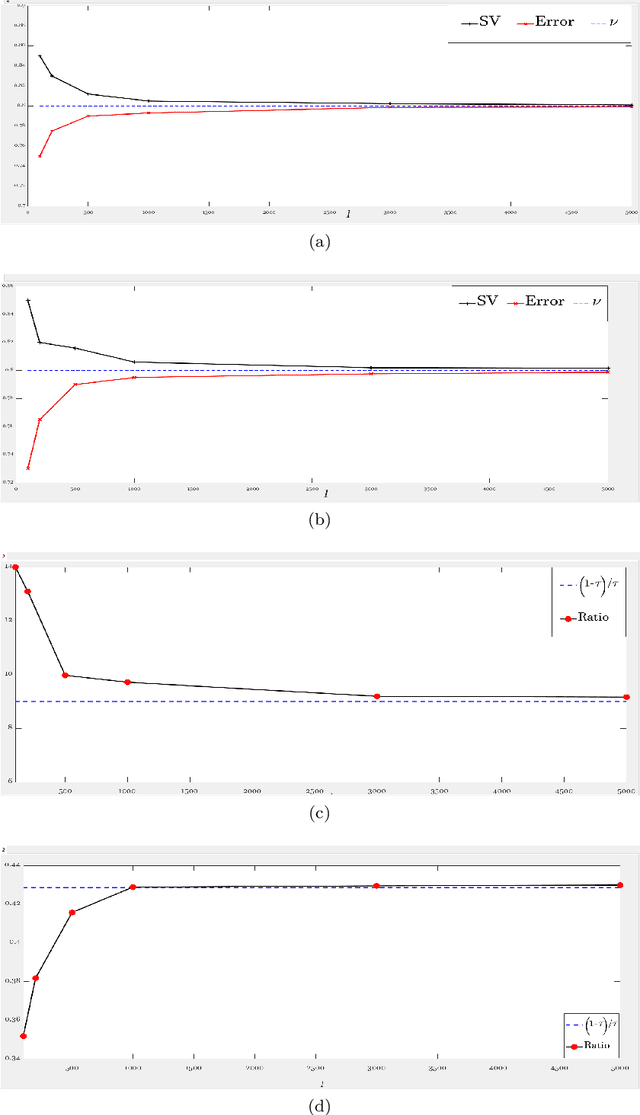
Abstract:This paper proposes a novel '$\nu$-support vector quantile regression' ($\nu$-SVQR) model for the quantile estimation. It can facilitate the automatic control over accuracy by creating a suitable asymmetric $\epsilon$-insensitive zone according to the variance present in data. The proposed $\nu$-SVQR model uses the $\nu$ fraction of training data points for the estimation of the quantiles. In the $\nu$-SVQR model, training points asymptotically appear above and below of the asymmetric $\epsilon$-insensitive tube in the ratio of $1-\tau$ and $\tau$. Further, there are other interesting properties of the proposed $\nu$-SVQR model, which we have briefly described in this paper. These properties have been empirically verified using the artificial and real world dataset also.
A new asymmetric $ε$-insensitive pinball loss function based support vector quantile regression model
Aug 19, 2019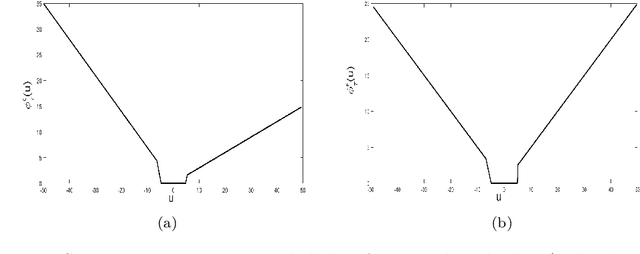
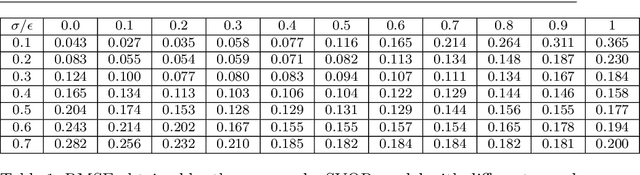
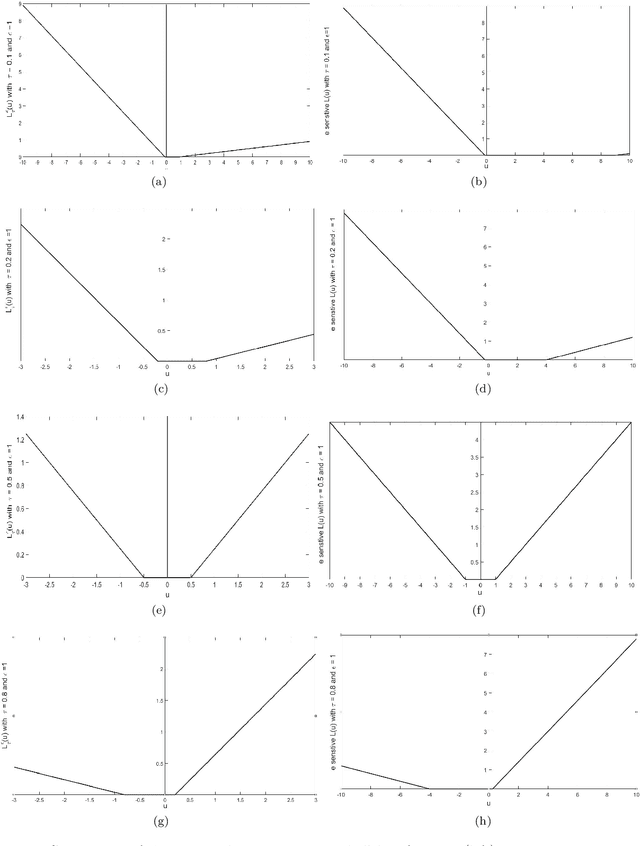
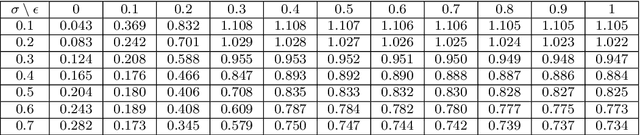
Abstract:In this paper, we propose a novel asymmetric $\epsilon$-insensitive pinball loss function for quantile estimation. There exists some pinball loss functions which attempt to incorporate the $\epsilon$-insensitive zone approach in it but, they fail to extend the $\epsilon$-insensitive approach for quantile estimation in true sense. The proposed asymmetric $\epsilon$-insensitive pinball loss function can make an asymmetric $\epsilon$- insensitive zone of fixed width around the data and divide it using $\tau$ value for the estimation of the $\tau$th quantile. The use of the proposed asymmetric $\epsilon$-insensitive pinball loss function in Support Vector Quantile Regression (SVQR) model improves its prediction ability significantly. It also brings the sparsity back in SVQR model. Further, the numerical results obtained by several experiments carried on artificial and real world datasets empirically show the efficacy of the proposed `$\epsilon$-Support Vector Quantile Regression' ($\epsilon$-SVQR) model over other existing SVQR models.
Support Vector Regression via a Combined Reward Cum Penalty Loss Function
Apr 28, 2019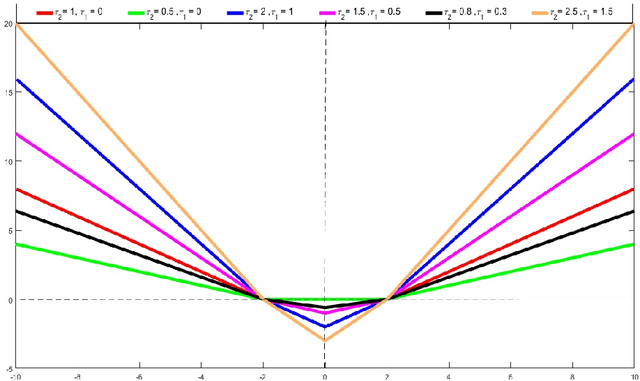
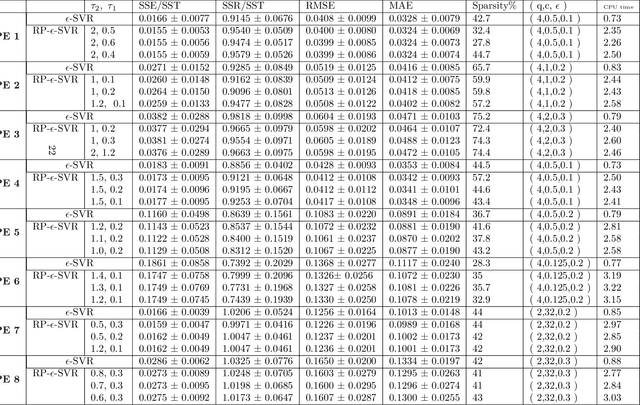
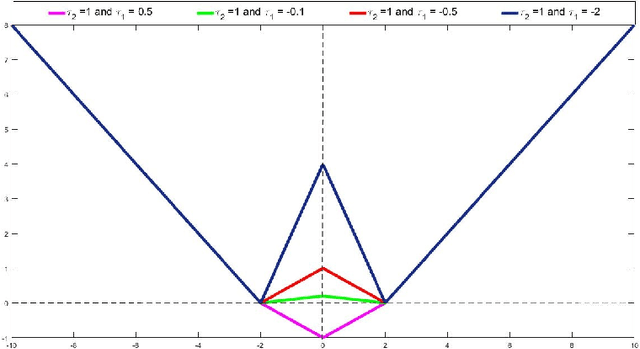
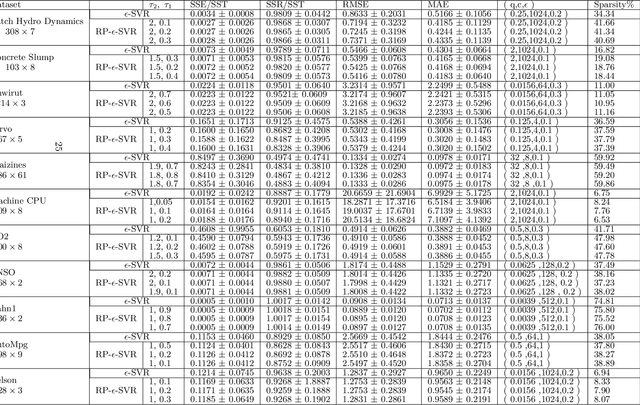
Abstract:In this paper, we introduce a novel combined reward cum penalty loss function to handle the regression problem. The proposed combined reward cum penalty loss function penalizes the data points which lie outside the $\epsilon$-tube of the regressor and also assigns reward for the data points which lie inside of the $\epsilon$-tube of the regressor. The combined reward cum penalty loss function based regression (RP-$\epsilon$-SVR) model has several interesting properties which are investigated in this paper and are also supported with the experimental results.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge