A $ν$- support vector quantile regression model with automatic accuracy control

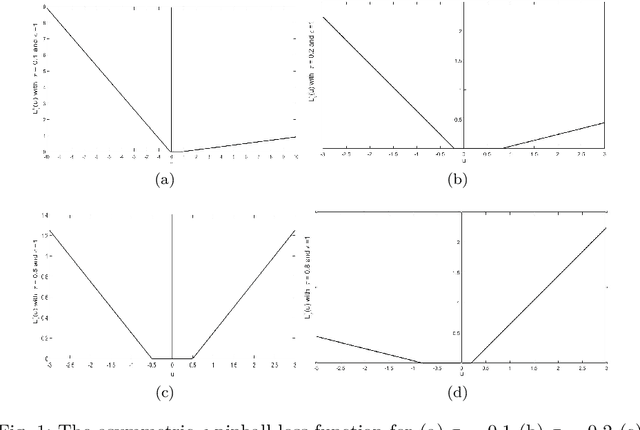
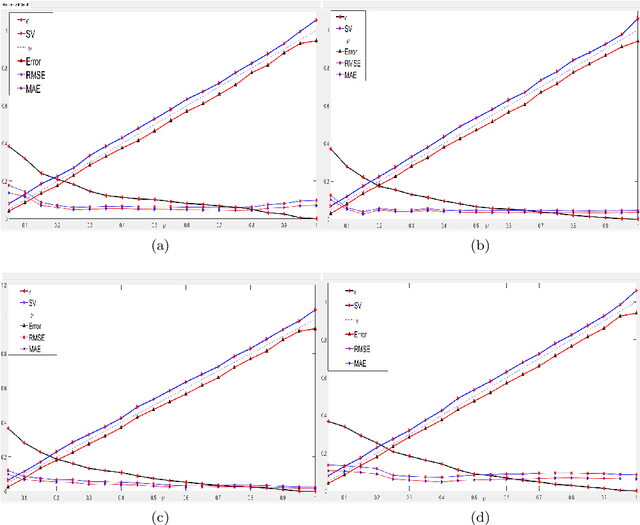
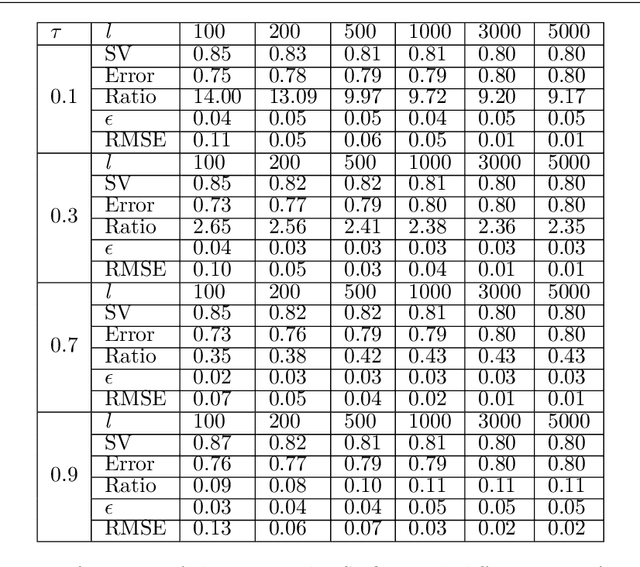
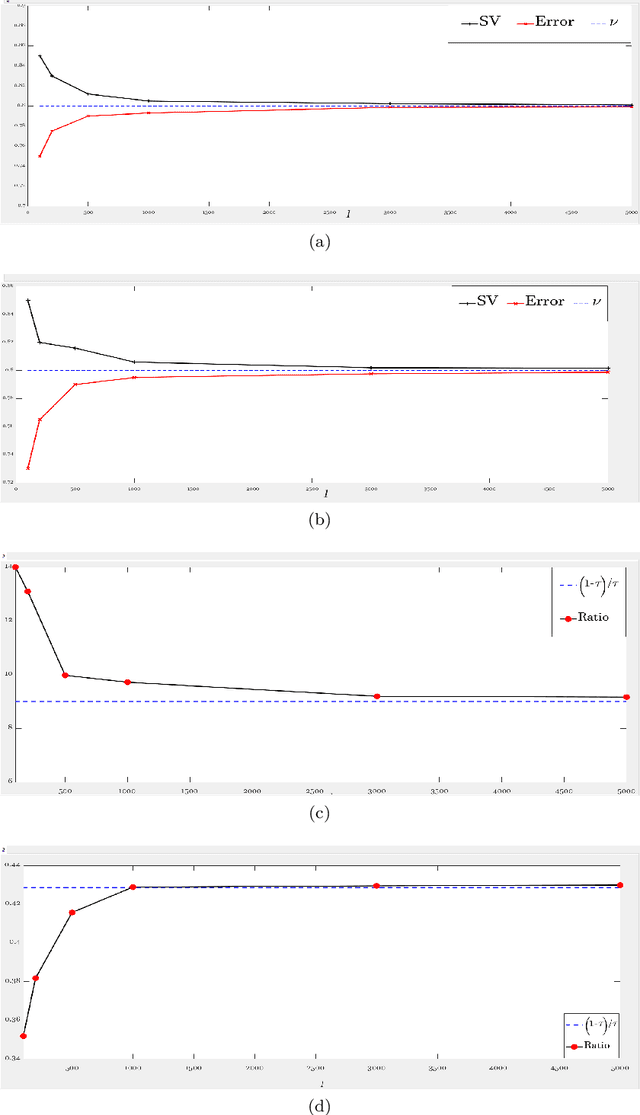
This paper proposes a novel '$\nu$-support vector quantile regression' ($\nu$-SVQR) model for the quantile estimation. It can facilitate the automatic control over accuracy by creating a suitable asymmetric $\epsilon$-insensitive zone according to the variance present in data. The proposed $\nu$-SVQR model uses the $\nu$ fraction of training data points for the estimation of the quantiles. In the $\nu$-SVQR model, training points asymptotically appear above and below of the asymmetric $\epsilon$-insensitive tube in the ratio of $1-\tau$ and $\tau$. Further, there are other interesting properties of the proposed $\nu$-SVQR model, which we have briefly described in this paper. These properties have been empirically verified using the artificial and real world dataset also.