Tube Loss based Deep Networks For Improving the Probabilistic Forecasting of Wind Speed

Uncertainty Quantification (UQ) in wind speed forecasting is a critical challenge in wind power production due to the inherently volatile nature of wind. By quantifying the associated risks and returns, UQ supports more effective decision-making for grid operations and participation in the electricity market. In this paper, we design a sequence of deep learning based probabilistic forecasting methods by using the Tube loss function for wind speed forecasting. The Tube loss function is a simple and model agnostic Prediction Interval (PI) estimation approach and can obtain the narrow PI with asymptotical coverage guarantees without any distribution assumption. Our deep probabilistic forecasting models effectively incorporate popular architectures such as LSTM, GRU, and TCN within the Tube loss framework. We further design a simple yet effective heuristic for tuning the $\delta$ parameter of the Tube loss function so that our deep forecasting models obtain the narrower PI without compromising its calibration ability. We have considered three wind datasets, containing the hourly recording of the wind speed, collected from three distinct location namely Jaisalmer, Los Angeles and San Fransico. Our numerical results demonstrate that the proposed deep forecasting models produce more reliable and narrower PIs compared to recently developed probabilistic wind forecasting methods.

Uncertainty Quantification in SVM prediction

This paper explores Uncertainty Quantification (UQ) in SVM predictions, particularly for regression and forecasting tasks. Unlike the Neural Network, the SVM solutions are typically more stable, sparse, optimal and interpretable. However, there are only few literature which addresses the UQ in SVM prediction. At first, we provide a comprehensive summary of existing Prediction Interval (PI) estimation and probabilistic forecasting methods developed in the SVM framework and evaluate them against the key properties expected from an ideal PI model. We find that none of the existing SVM PI models achieves a sparse solution. To introduce sparsity in SVM model, we propose the Sparse Support Vector Quantile Regression (SSVQR) model, which constructs PIs and probabilistic forecasts by solving a pair of linear programs. Further, we develop a feature selection algorithm for PI estimation using SSVQR that effectively eliminates a significant number of features while improving PI quality in case of high-dimensional dataset. Finally we extend the SVM models in Conformal Regression setting for obtaining more stable prediction set with finite test set guarantees. Extensive experiments on artificial, real-world benchmark datasets compare the different characteristics of both existing and proposed SVM-based PI estimation methods and also highlight the advantages of the feature selection in PI estimation. Furthermore, we compare both, the existing and proposed SVM-based PI estimation models, with modern deep learning models for probabilistic forecasting tasks on benchmark datasets. Furthermore, SVM models show comparable or superior performance to modern complex deep learning models for probabilistic forecasting task in our experiments.

Tube Loss: A Novel Approach for Prediction Interval Estimation and probabilistic forecasting

This paper proposes a novel loss function, called 'Tube Loss', for simultaneous estimation of bounds of a Prediction Interval (PI) in the regression setup, and also for generating probabilistic forecasts from time series data solving a single optimization problem. The PIs obtained by minimizing the empirical risk based on the Tube Loss are shown to be of better quality than the PIs obtained by the existing methods in the following sense. First, it yields intervals that attain the prespecified confidence level $t \in(0,1)$ asymptotically. A theoretical proof of this fact is given. Secondly, the user is allowed to move the interval up or down by controlling the value of a parameter. This helps the user to choose a PI capturing denser regions of the probability distribution of the response variable inside the interval, and thus, sharpening its width. This is shown to be especially useful when the conditional distribution of the response variable is skewed. Further, the Tube Loss based PI estimation method can trade-off between the coverage and the average width by solving a single optimization problem. It enables further reduction of the average width of PI through re-calibration. Also, unlike a few existing PI estimation methods the gradient descent (GD) method can be used for minimization of empirical risk. Finally, through extensive experimentation, we have shown the efficacy of the Tube Loss based PI estimation in kernel machines, neural networks and deep networks and also for probabilistic forecasting tasks. The codes of the experiments are available at https://github.com/ltpritamanand/Tube_loss

Improvement over Pinball Loss Support Vector Machine

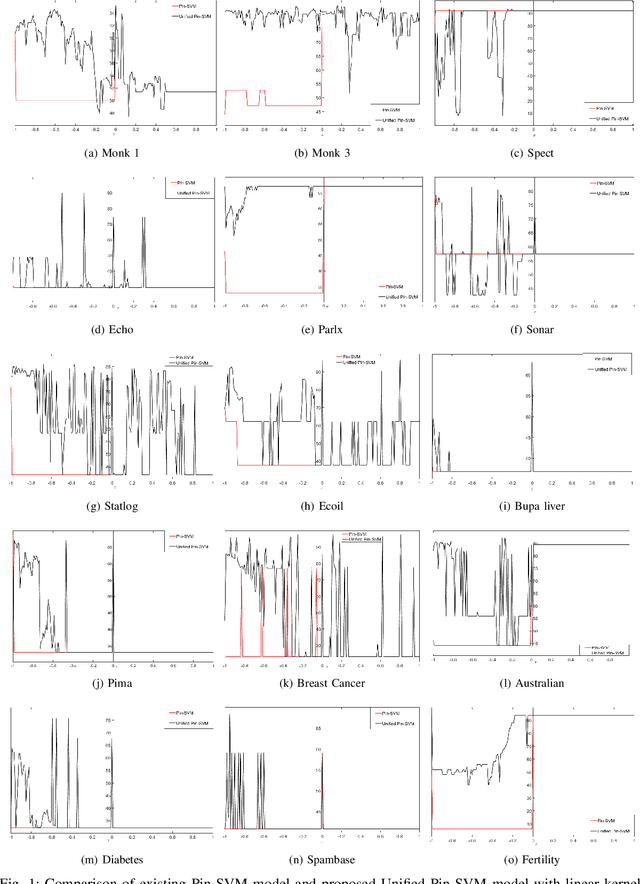
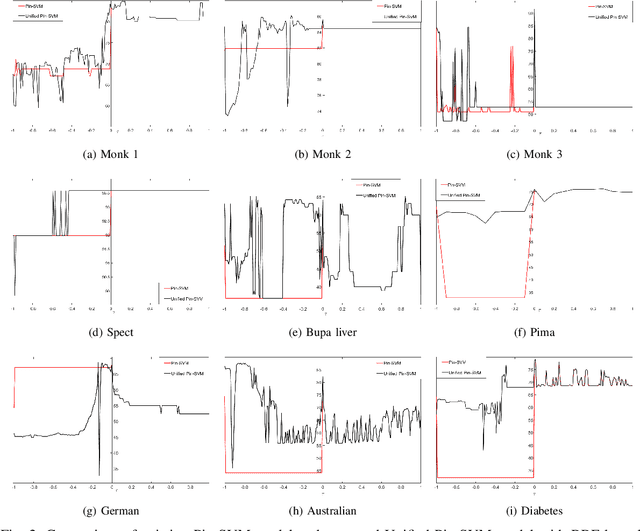
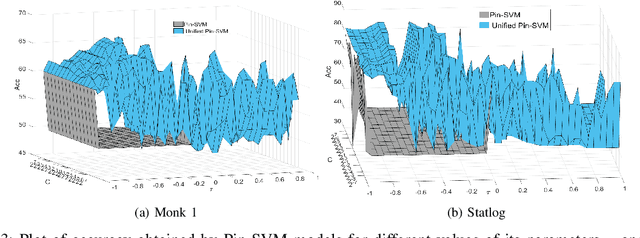
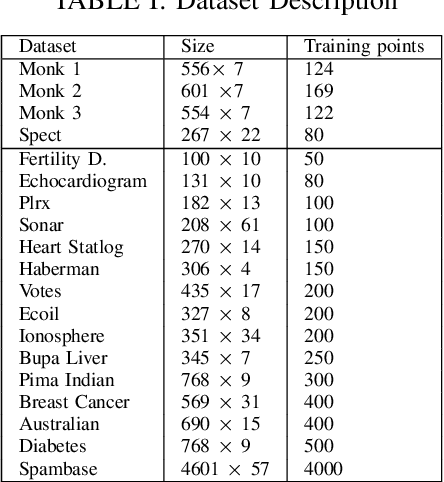
Recently, there have been several papers that discuss the extension of the Pinball loss Support Vector Machine (Pin-SVM) model, originally proposed by Huang et al.,[1][2]. Pin-SVM classifier deals with the pinball loss function, which has been defined in terms of the parameter $\tau$. The parameter $\tau$ can take values in $[ -1,1]$. The existing Pin-SVM model requires to solve the same optimization problem for all values of $\tau$ in $[ -1,1]$. In this paper, we improve the existing Pin-SVM model for the binary classification task. At first, we note that there is major difficulty in Pin-SVM model (Huang et al. [1]) for $ -1 \leq \tau < 0$. Specifically, we show that the Pin-SVM model requires the solution of different optimization problem for $ -1 \leq \tau < 0$. We further propose a unified model termed as Unified Pin-SVM which results in a QPP valid for all $-1\leq \tau \leq 1$ and hence more convenient to use. The proposed Unified Pin-SVM model can obtain a significant improvement in accuracy over the existing Pin-SVM model which has also been empirically justified by extensive numerical experiments with real-world datasets.

Learning a powerful SVM using piece-wise linear loss functions

In this paper, we have considered general k-piece-wise linear convex loss functions in SVM model for measuring the empirical risk. The resulting k-Piece-wise Linear loss Support Vector Machine (k-PL-SVM) model is an adaptive SVM model which can learn a suitable piece-wise linear loss function according to nature of the given training set. The k-PL-SVM models are general SVM models and existing popular SVM models, like C-SVM, LS-SVM and Pin-SVM models, are their particular cases. We have performed the extensive numerical experiments with k-PL-SVM models for k = 2 and 3 and shown that they are improvement over existing SVM models.

A $ν$- support vector quantile regression model with automatic accuracy control

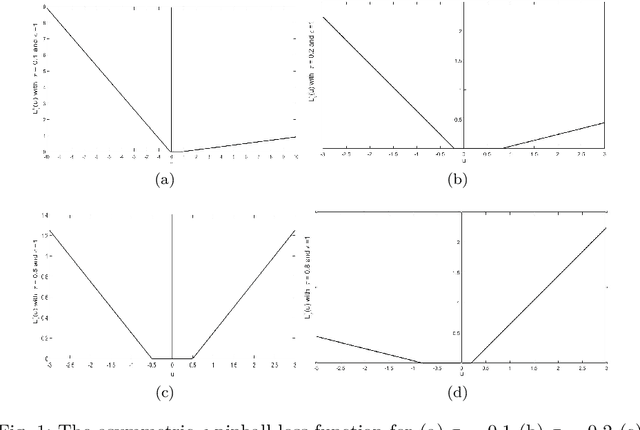
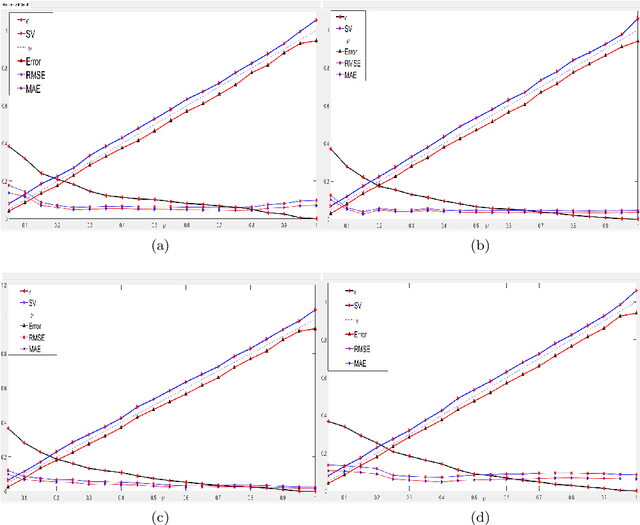
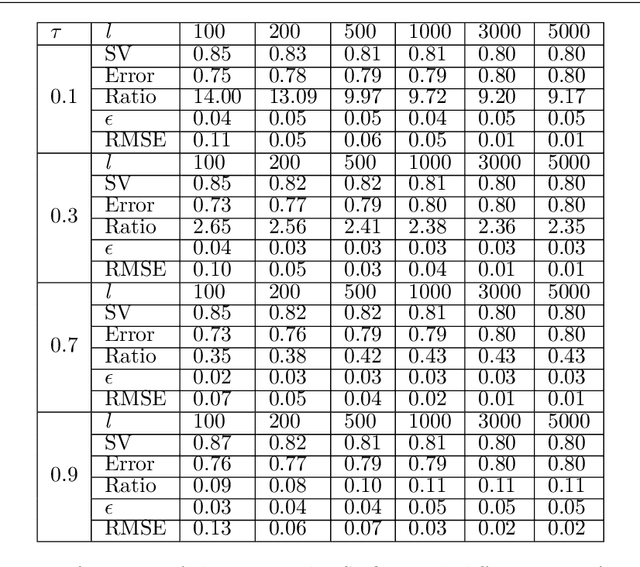
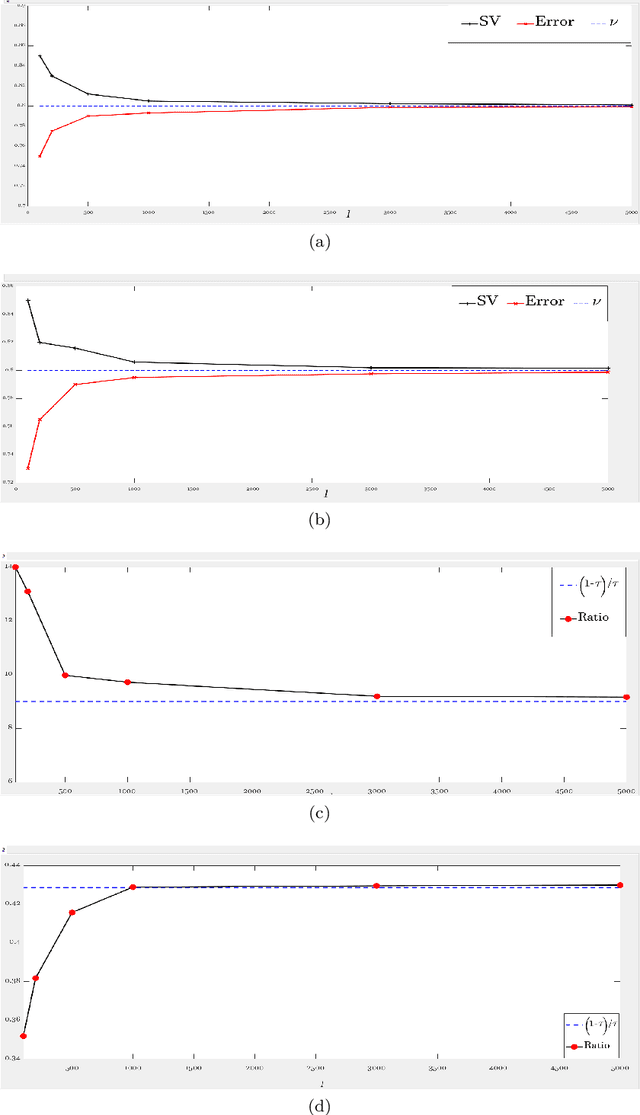
This paper proposes a novel '$\nu$-support vector quantile regression' ($\nu$-SVQR) model for the quantile estimation. It can facilitate the automatic control over accuracy by creating a suitable asymmetric $\epsilon$-insensitive zone according to the variance present in data. The proposed $\nu$-SVQR model uses the $\nu$ fraction of training data points for the estimation of the quantiles. In the $\nu$-SVQR model, training points asymptotically appear above and below of the asymmetric $\epsilon$-insensitive tube in the ratio of $1-\tau$ and $\tau$. Further, there are other interesting properties of the proposed $\nu$-SVQR model, which we have briefly described in this paper. These properties have been empirically verified using the artificial and real world dataset also.

A new asymmetric $ε$-insensitive pinball loss function based support vector quantile regression model

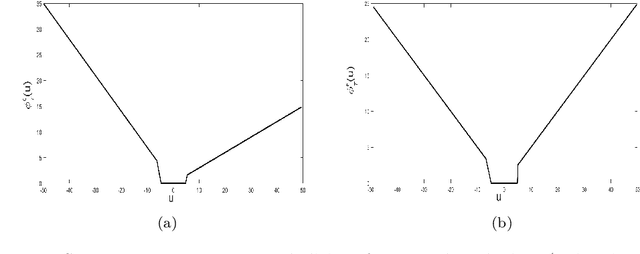
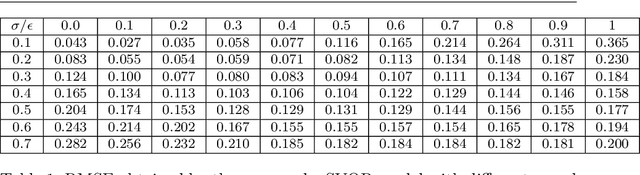
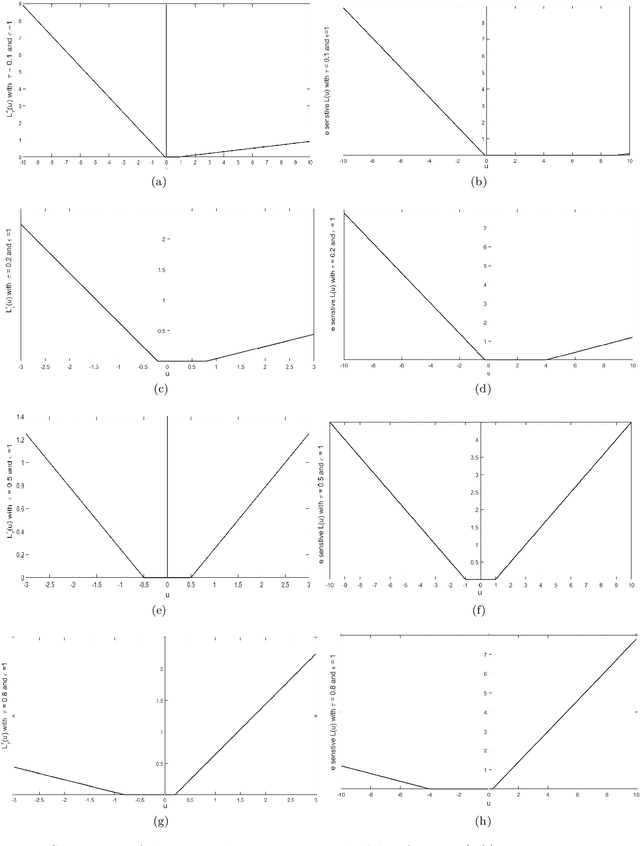
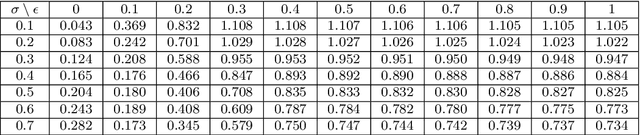
In this paper, we propose a novel asymmetric $\epsilon$-insensitive pinball loss function for quantile estimation. There exists some pinball loss functions which attempt to incorporate the $\epsilon$-insensitive zone approach in it but, they fail to extend the $\epsilon$-insensitive approach for quantile estimation in true sense. The proposed asymmetric $\epsilon$-insensitive pinball loss function can make an asymmetric $\epsilon$- insensitive zone of fixed width around the data and divide it using $\tau$ value for the estimation of the $\tau$th quantile. The use of the proposed asymmetric $\epsilon$-insensitive pinball loss function in Support Vector Quantile Regression (SVQR) model improves its prediction ability significantly. It also brings the sparsity back in SVQR model. Further, the numerical results obtained by several experiments carried on artificial and real world datasets empirically show the efficacy of the proposed `$\epsilon$-Support Vector Quantile Regression' ($\epsilon$-SVQR) model over other existing SVQR models.

Support Vector Regression via a Combined Reward Cum Penalty Loss Function

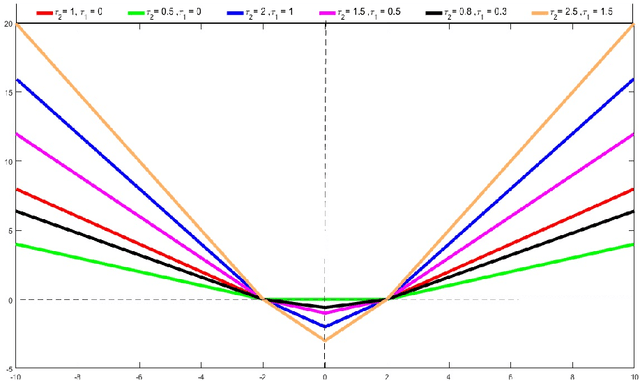
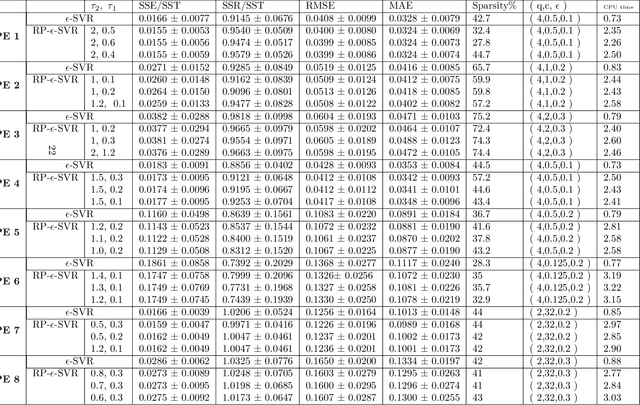
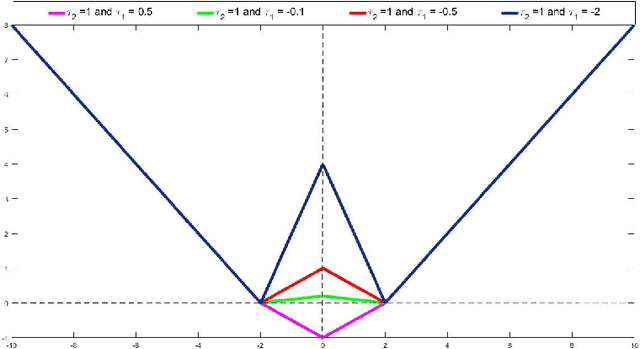
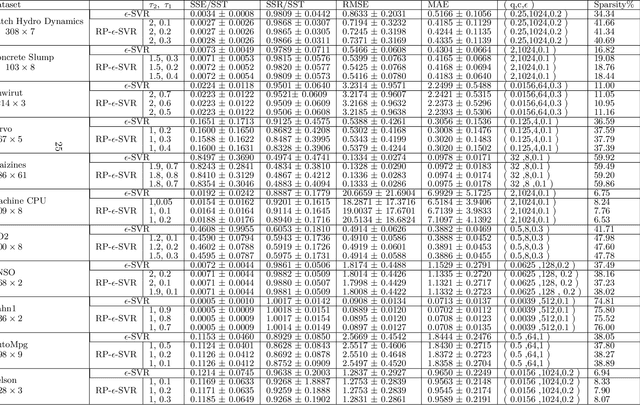
In this paper, we introduce a novel combined reward cum penalty loss function to handle the regression problem. The proposed combined reward cum penalty loss function penalizes the data points which lie outside the $\epsilon$-tube of the regressor and also assigns reward for the data points which lie inside of the $\epsilon$-tube of the regressor. The combined reward cum penalty loss function based regression (RP-$\epsilon$-SVR) model has several interesting properties which are investigated in this paper and are also supported with the experimental results.