Improvement over Pinball Loss Support Vector Machine
Paper and Code
Jun 02, 2021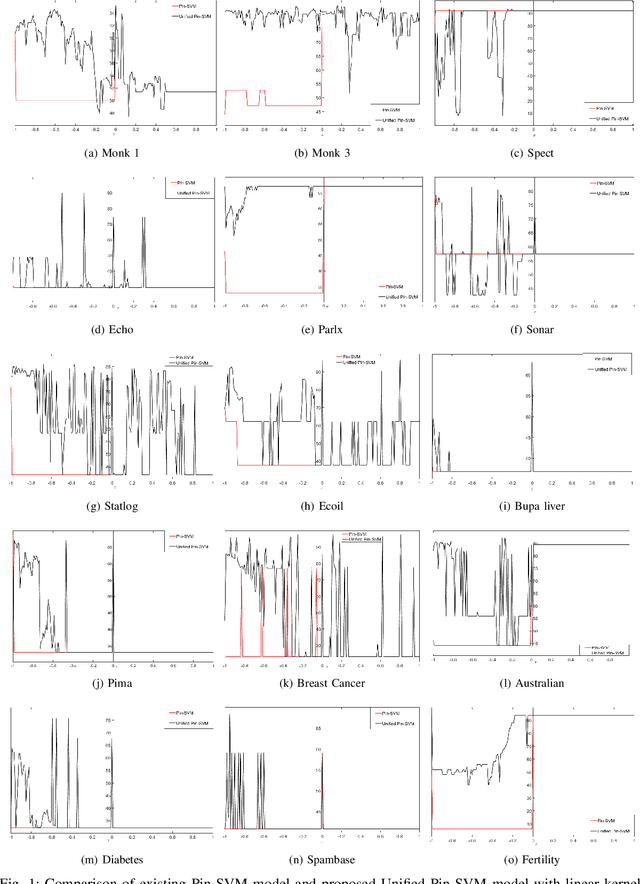
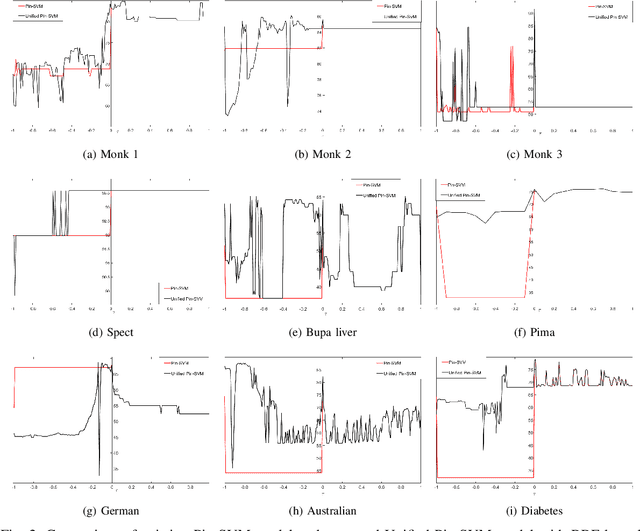
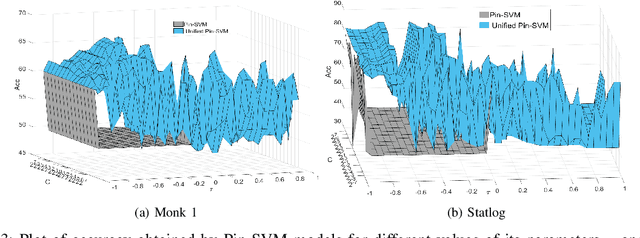
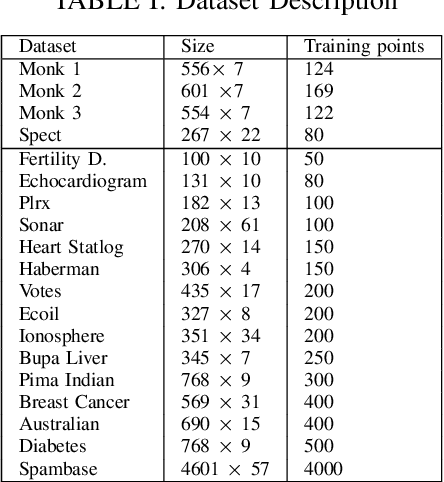
Recently, there have been several papers that discuss the extension of the Pinball loss Support Vector Machine (Pin-SVM) model, originally proposed by Huang et al.,[1][2]. Pin-SVM classifier deals with the pinball loss function, which has been defined in terms of the parameter $\tau$. The parameter $\tau$ can take values in $[ -1,1]$. The existing Pin-SVM model requires to solve the same optimization problem for all values of $\tau$ in $[ -1,1]$. In this paper, we improve the existing Pin-SVM model for the binary classification task. At first, we note that there is major difficulty in Pin-SVM model (Huang et al. [1]) for $ -1 \leq \tau < 0$. Specifically, we show that the Pin-SVM model requires the solution of different optimization problem for $ -1 \leq \tau < 0$. We further propose a unified model termed as Unified Pin-SVM which results in a QPP valid for all $-1\leq \tau \leq 1$ and hence more convenient to use. The proposed Unified Pin-SVM model can obtain a significant improvement in accuracy over the existing Pin-SVM model which has also been empirically justified by extensive numerical experiments with real-world datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge