GBSVR: Granular Ball Support Vector Regression
Paper and Code
Mar 13, 2025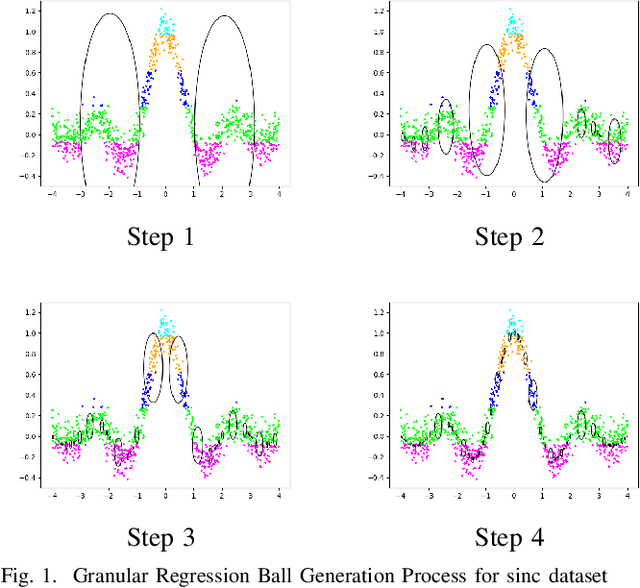

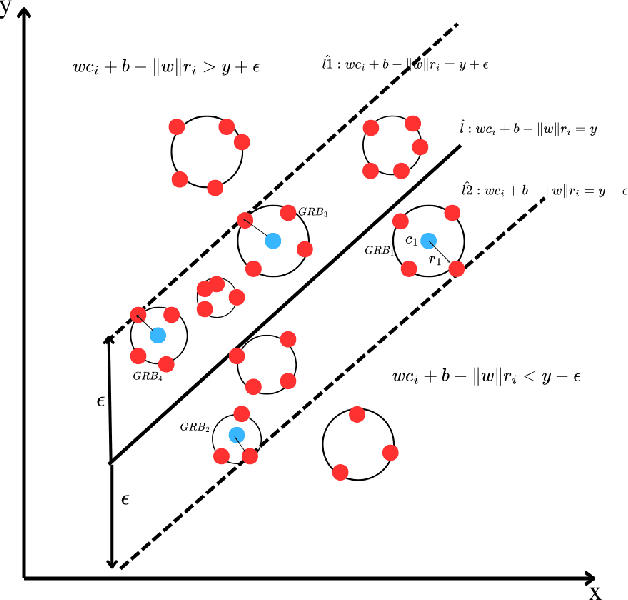
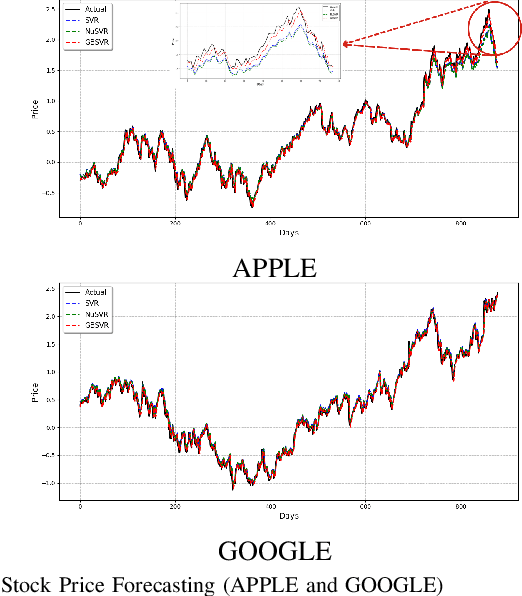
Support Vector Regression (SVR) and its variants are widely used to handle regression tasks, however, since their solution involves solving an expensive quadratic programming problem, it limits its application, especially when dealing with large datasets. Additionally, SVR uses an epsilon-insensitive loss function which is sensitive to outliers and therefore can adversely affect its performance. We propose Granular Ball Support Vector Regression (GBSVR) to tackle problem of regression by using granular ball concept. These balls are useful in simplifying complex data spaces for machine learning tasks, however, to the best of our knowledge, they have not been sufficiently explored for regression problems. Granular balls group the data points into balls based on their proximity and reduce the computational cost in SVR by replacing the large number of data points with far fewer granular balls. This work also suggests a discretization method for continuous-valued attributes to facilitate the construction of granular balls. The effectiveness of the proposed approach is evaluated on several benchmark datasets and it outperforms existing state-of-the-art approaches
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge