Statistical Analysis of the Sinkhorn Iterations for Two-Sample Schrödinger Bridge Estimation

The Schr\"odinger bridge problem seeks the optimal stochastic process that connects two given probability distributions with minimal energy modification. While the Sinkhorn algorithm is widely used to solve the static optimal transport problem, a recent work (Pooladian and Niles-Weed, 2024) proposed the Sinkhorn bridge, which estimates Schr\"odinger bridges by plugging optimal transport into the time-dependent drifts of SDEs, with statistical guarantees in the one-sample estimation setting where the true source distribution is fully accessible. In this work, to further justify this method, we study the statistical performance of intermediate Sinkhorn iterations in the two-sample estimation setting, where only finite samples from both source and target distributions are available. Specifically, we establish a statistical bound on the squared total variation error of Sinkhorn bridge iterations: $O(1/m+1/n + r^{4k})~(r \in (0,1))$, where $m$ and $n$ are the sample sizes from the source and target distributions, respectively, and $k$ is the number of Sinkhorn iterations. This result provides a theoretical guarantee for the finite-sample performance of the Schr\"odinger bridge estimator and offers practical guidance for selecting sample sizes and the number of Sinkhorn iterations. Notably, our theoretical results apply to several representative methods such as [SF]$^2$M, DSBM-IMF, BM2, and LightSB(-M) under specific settings, through the previously unnoticed connection between these estimators.

Optimal Transport Barycenter via Nonconvex-Concave Minimax Optimization

The optimal transport barycenter (a.k.a. Wasserstein barycenter) is a fundamental notion of averaging that extends from the Euclidean space to the Wasserstein space of probability distributions. Computation of the unregularized barycenter for discretized probability distributions on point clouds is a challenging task when the domain dimension $d > 1$. Most practical algorithms for approximating the barycenter problem are based on entropic regularization. In this paper, we introduce a nearly linear time $O(m \log{m})$ and linear space complexity $O(m)$ primal-dual algorithm, the Wasserstein-Descent $\dot{\mathbb{H}}^1$-Ascent (WDHA) algorithm, for computing the exact barycenter when the input probability density functions are discretized on an $m$-point grid. The key success of the WDHA algorithm hinges on alternating between two different yet closely related Wasserstein and Sobolev optimization geometries for the primal barycenter and dual Kantorovich potential subproblems. Under reasonable assumptions, we establish the convergence rate and iteration complexity of WDHA to its stationary point when the step size is appropriately chosen. Superior computational efficacy, scalability, and accuracy over the existing Sinkhorn-type algorithms are demonstrated on high-resolution (e.g., $1024 \times 1024$ images) 2D synthetic and real data.

A Gromov--Wasserstein Geometric View of Spectrum-Preserving Graph Coarsening

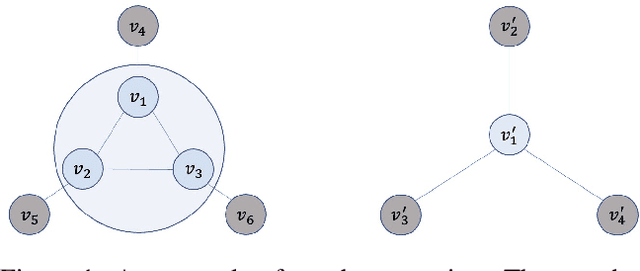
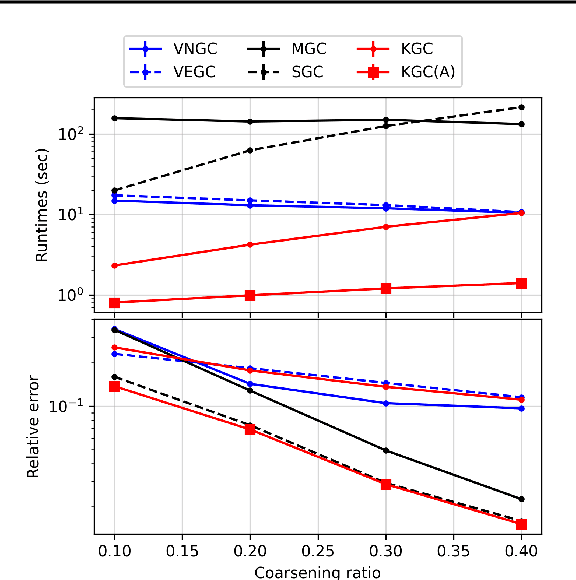
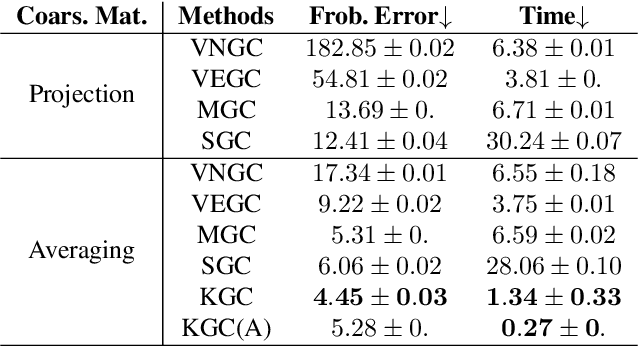
Graph coarsening is a technique for solving large-scale graph problems by working on a smaller version of the original graph, and possibly interpolating the results back to the original graph. It has a long history in scientific computing and has recently gained popularity in machine learning, particularly in methods that preserve the graph spectrum. This work studies graph coarsening from a different perspective, developing a theory for preserving graph distances and proposing a method to achieve this. The geometric approach is useful when working with a collection of graphs, such as in graph classification and regression. In this study, we consider a graph as an element on a metric space equipped with the Gromov--Wasserstein (GW) distance, and bound the difference between the distance of two graphs and their coarsened versions. Minimizing this difference can be done using the popular weighted kernel $K$-means method, which improves existing spectrum-preserving methods with the proper choice of the kernel. The study includes a set of experiments to support the theory and method, including approximating the GW distance, preserving the graph spectrum, classifying graphs using spectral information, and performing regression using graph convolutional networks. Code is available at https://github.com/ychen-stat-ml/GW-Graph-Coarsening .

Mean field Variational Inference via Wasserstein Gradient Flow

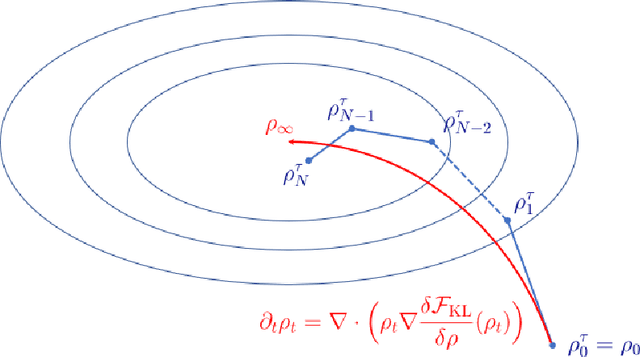
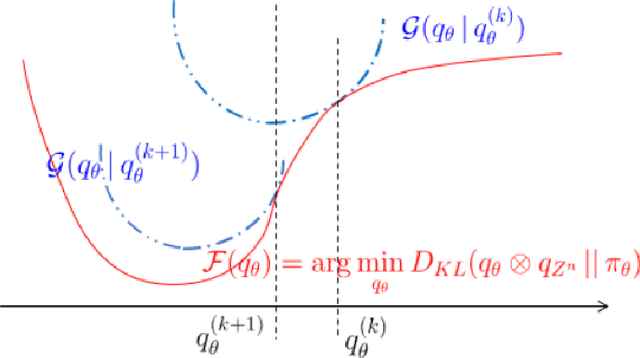
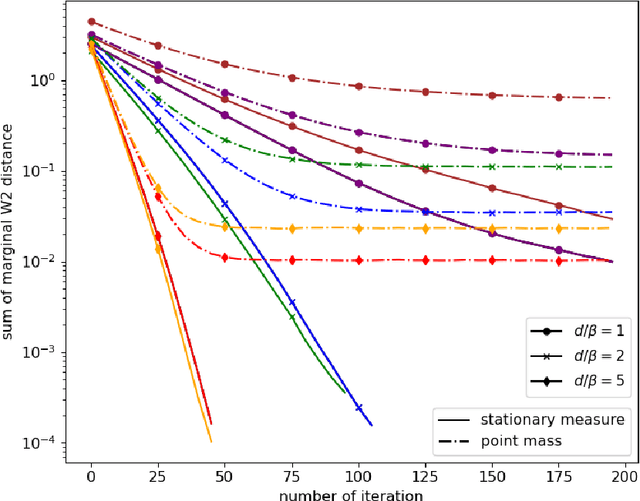
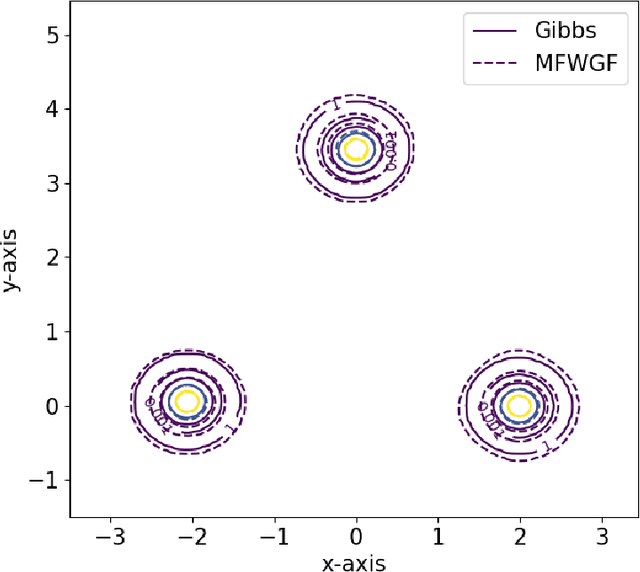
Variational inference (VI) provides an appealing alternative to traditional sampling-based approaches for implementing Bayesian inference due to its conceptual simplicity, statistical accuracy and computational scalability. However, common variational approximation schemes, such as the mean-field (MF) approximation, require certain conjugacy structure to facilitate efficient computation, which may add unnecessary restrictions to the viable prior distribution family and impose further constraints on the variational approximation family. In this work, we develop a general computational framework for implementing MF-VI via Wasserstein gradient flow (WGF), a gradient flow over the space of probability measures. When specialized to Bayesian latent variable models, we analyze the algorithmic convergence of an alternating minimization scheme based on a time-discretized WGF for implementing the MF approximation. In particular, the proposed algorithm resembles a distributional version of EM algorithm, consisting of an E-step of updating the latent variable variational distribution and an M-step of conducting steepest descent over the variational distribution of parameters. Our theoretical analysis relies on optimal transport theory and subdifferential calculus in the space of probability measures. We prove the exponential convergence of the time-discretized WGF for minimizing a generic objective functional given strict convexity along generalized geodesics. We also provide a new proof of the exponential contraction of the variational distribution obtained from the MF approximation by using the fixed-point equation of the time-discretized WGF. We apply our method and theory to two classic Bayesian latent variable models, the Gaussian mixture model and the mixture of regression model. Numerical experiments are also conducted to compliment the theoretical findings under these two models.