Graph Based Multi-layer K-means++ for Sensory Pattern Analysis in Constrained Spaces

In this paper, we focus on developing a novel unsupervised machine learning algorithm, named graph based multi-layer k-means++ (G-MLKM), to solve data-target association problem when targets move on a constrained space and minimal information of the targets can be obtained by sensors. Instead of employing the traditional data-target association methods that are based on statistical probabilities, the G-MLKM solves the problem via data clustering. We first will develop the Multi-layer K-means++ (MLKM) method for data-target association at local space given a simplified constrained space situation. Then a p-dual graph is proposed to represent the general constrained space when local spaces are interconnected. Based on the dual graph and graph theory, we then generalize MLKM to G-MLKM by first understanding local data-target association and then extracting cross-local data-target association mathematically analyze the data association at intersections of that space. To exclude potential data-target association errors that disobey physical rules, we also develop error correction mechanisms to further improve the accuracy. Numerous simulation examples are conducted to demonstrate the performance of G-MLKM.

A Multi-Layer K-means Approach for Multi-Sensor Data Pattern Recognition in Multi-Target Localization

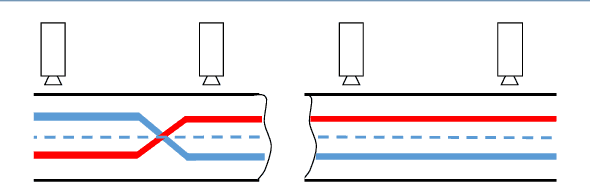
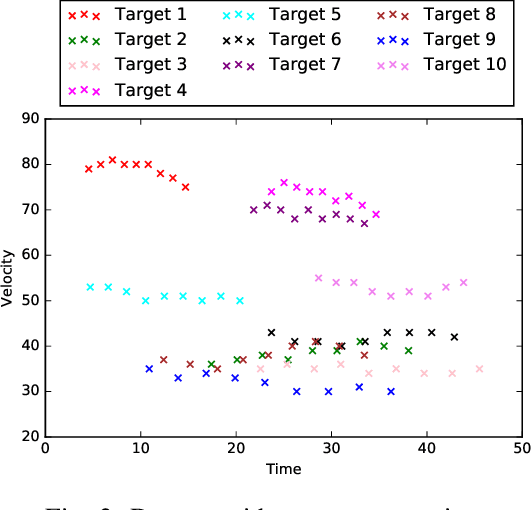
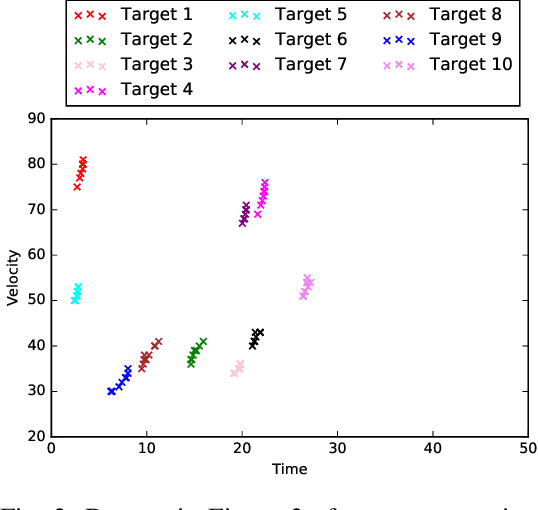
Data-target association is an important step in multi-target localization for the intelligent operation of un- manned systems in numerous applications such as search and rescue, traffic management and surveillance. The objective of this paper is to present an innovative data association learning approach named multi-layer K-means (MLKM) based on leveraging the advantages of some existing machine learning approaches, including K-means, K-means++, and deep neural networks. To enable the accurate data association from different sensors for efficient target localization, MLKM relies on the clustering capabilities of K-means++ structured in a multi-layer framework with the error correction feature that is motivated by the backpropogation that is well-known in deep learning research. To show the effectiveness of the MLKM method, numerous simulation examples are conducted to compare its performance with K-means, K-means++, and deep neural networks.