Quantum Adjoint Convolutional Layers for Effective Data Representation

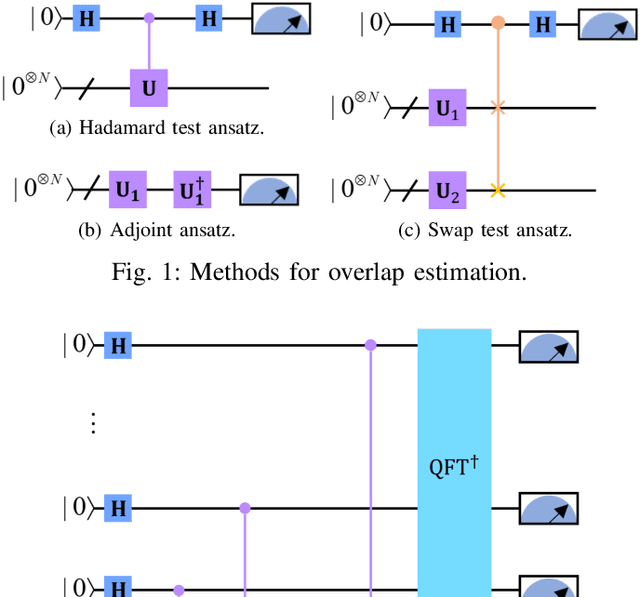
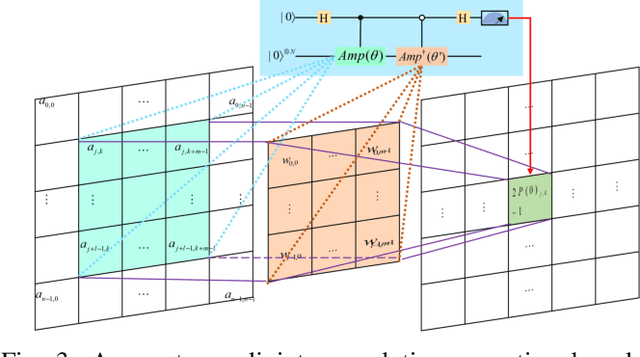
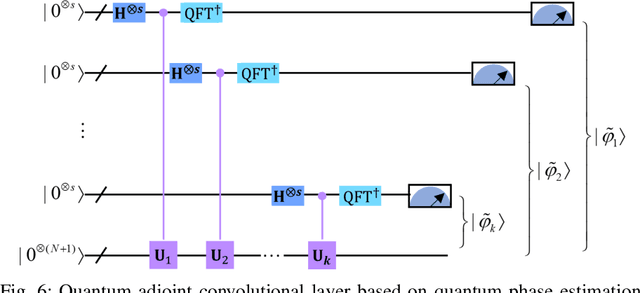
Quantum Convolutional Layer (QCL) is considered as one of the core of Quantum Convolutional Neural Networks (QCNNs) due to its efficient data feature extraction capability. However, the current principle of QCL is not as mathematically understandable as Classical Convolutional Layer (CCL) due to its black-box structure. Moreover, classical data mapping in many QCLs is inefficient. To this end, firstly, the Quantum Adjoint Convolution Operation (QACO) consisting of a quantum amplitude encoding and its inverse is theoretically shown to be equivalent to the quantum normalization of the convolution operation based on the Frobenius inner product while achieving an efficient characterization of the data. Subsequently, QACO is extended into a Quantum Adjoint Convolutional Layer (QACL) by Quantum Phase Estimation (QPE) to compute all Frobenius inner products in parallel. At last, comparative simulation experiments are carried out on PennyLane and TensorFlow platforms, mainly for the two cases of kernel fixed and unfixed in QACL. The results demonstrate that QACL with the insight of special quantum properties for the same images, provides higher training accuracy in MNIST and Fashion MNIST classification experiments, but sacrifices the learning performance to some extent. Predictably, our research lays the foundation for the development of efficient and interpretable quantum convolutional networks and also advances the field of quantum machine vision.

GQHAN: A Grover-inspired Quantum Hard Attention Network

Numerous current Quantum Machine Learning (QML) models exhibit an inadequacy in discerning the significance of quantum data, resulting in diminished efficacy when handling extensive quantum datasets. Hard Attention Mechanism (HAM), anticipated to efficiently tackle the above QML bottlenecks, encounters the substantial challenge of non-differentiability, consequently constraining its extensive applicability. In response to the dilemma of HAM and QML, a Grover-inspired Quantum Hard Attention Mechanism (GQHAM) consisting of a Flexible Oracle (FO) and an Adaptive Diffusion Operator (ADO) is proposed. Notably, the FO is designed to surmount the non-differentiable issue by executing the activation or masking of Discrete Primitives (DPs) with Flexible Control (FC) to weave various discrete destinies. Based on this, such discrete choice can be visualized with a specially defined Quantum Hard Attention Score (QHAS). Furthermore, a trainable ADO is devised to boost the generality and flexibility of GQHAM. At last, a Grover-inspired Quantum Hard Attention Network (GQHAN) based on QGHAM is constructed on PennyLane platform for Fashion MNIST binary classification. Experimental findings demonstrate that GQHAN adeptly surmounts the non-differentiability hurdle, surpassing the efficacy of extant quantum soft self-attention mechanisms in accuracies and learning ability. In noise experiments, GQHAN is robuster to bit-flip noise in accuracy and amplitude damping noise in learning performance. Predictably, the proposal of GQHAN enriches the Quantum Attention Mechanism (QAM), lays the foundation for future quantum computers to process large-scale data, and promotes the development of quantum computer vision.

QKSAN: A Quantum Kernel Self-Attention Network

Self-Attention Mechanism (SAM) is skilled at extracting important information from the interior of data to improve the computational efficiency of models. Nevertheless, many Quantum Machine Learning (QML) models lack the ability to distinguish the intrinsic connections of information like SAM, which limits their effectiveness on massive high-dimensional quantum data. To address this issue, a Quantum Kernel Self-Attention Mechanism (QKSAM) is introduced, which combines the data representation benefit of Quantum Kernel Methods (QKM) with the efficient information extraction capability of SAM. A Quantum Kernel Self-Attention Network (QKSAN) framework is built based on QKSAM, with Deferred Measurement Principle (DMP) and conditional measurement techniques, which releases half of the quantum resources with probabilistic measurements during computation. The Quantum Kernel Self-Attention Score (QKSAS) determines the measurement conditions and reflects the probabilistic nature of quantum systems. Finally, four QKSAN models are deployed on the Pennylane platform to perform binary classification on MNIST images. The best-performing among the four models is assessed for noise immunity and learning ability. Remarkably, the potential learning benefit of partial QKSAN models over classical deep learning is that they require few parameters for a high return of 98\% $\pm$ 1\% test and train accuracy, even with highly compressed images. QKSAN lays the foundation for future quantum computers to perform machine learning on massive amounts of data, while driving advances in areas such as quantum Natural Language Processing (NLP).