Quantum Adjoint Convolutional Layers for Effective Data Representation
Paper and Code
Apr 26, 2024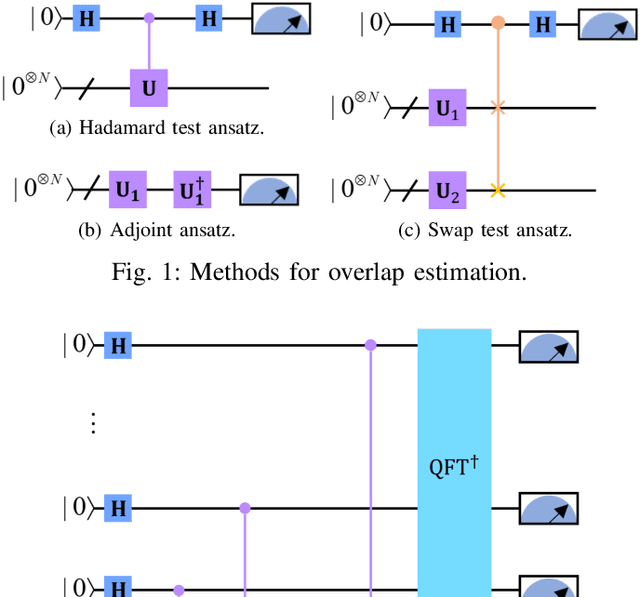
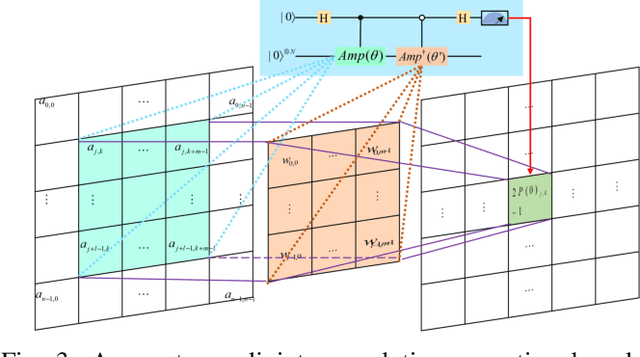
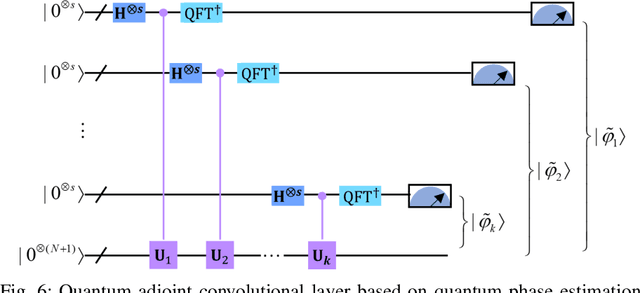
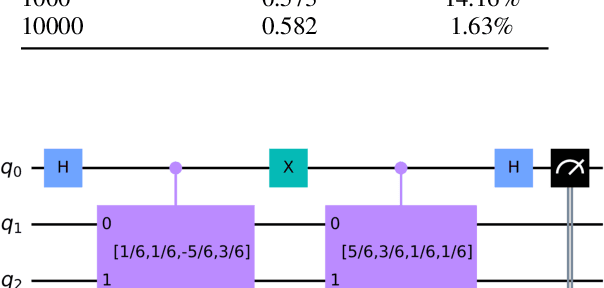
Quantum Convolutional Layer (QCL) is considered as one of the core of Quantum Convolutional Neural Networks (QCNNs) due to its efficient data feature extraction capability. However, the current principle of QCL is not as mathematically understandable as Classical Convolutional Layer (CCL) due to its black-box structure. Moreover, classical data mapping in many QCLs is inefficient. To this end, firstly, the Quantum Adjoint Convolution Operation (QACO) consisting of a quantum amplitude encoding and its inverse is theoretically shown to be equivalent to the quantum normalization of the convolution operation based on the Frobenius inner product while achieving an efficient characterization of the data. Subsequently, QACO is extended into a Quantum Adjoint Convolutional Layer (QACL) by Quantum Phase Estimation (QPE) to compute all Frobenius inner products in parallel. At last, comparative simulation experiments are carried out on PennyLane and TensorFlow platforms, mainly for the two cases of kernel fixed and unfixed in QACL. The results demonstrate that QACL with the insight of special quantum properties for the same images, provides higher training accuracy in MNIST and Fashion MNIST classification experiments, but sacrifices the learning performance to some extent. Predictably, our research lays the foundation for the development of efficient and interpretable quantum convolutional networks and also advances the field of quantum machine vision.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge