Kandinsky Conformal Prediction: Efficient Calibration of Image Segmentation Algorithms

Image segmentation algorithms can be understood as a collection of pixel classifiers, for which the outcomes of nearby pixels are correlated. Classifier models can be calibrated using Inductive Conformal Prediction, but this requires holding back a sufficiently large calibration dataset for computing the distribution of non-conformity scores of the model's predictions. If one only requires only marginal calibration on the image level, this calibration set consists of all individual pixels in the images available for calibration. However, if the goal is to attain proper calibration for each individual pixel classifier, the calibration set consists of individual images. In a scenario where data are scarce (such as the medical domain), it may not always be possible to set aside sufficiently many images for this pixel-level calibration. The method we propose, dubbed ``Kandinsky calibration'', makes use of the spatial structure present in the distribution of natural images to simultaneously calibrate the classifiers of ``similar'' pixels. This can be seen as an intermediate approach between marginal (imagewise) and conditional (pixelwise) calibration, where non-conformity scores are aggregated over similar image regions, thereby making more efficient use of the images available for calibration. We run experiments on segmentation algorithms trained and calibrated on subsets of the public MS-COCO and Medical Decathlon datasets, demonstrating that Kandinsky calibration method can significantly improve the coverage. When compared to both pixelwise and imagewise calibration on little data, the Kandinsky method achieves much lower coverage errors, indicating the data efficiency of the Kandinsky calibration.

Constrained Empirical Risk Minimization: Theory and Practice

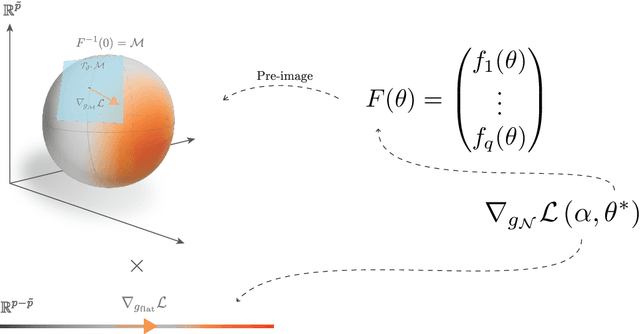
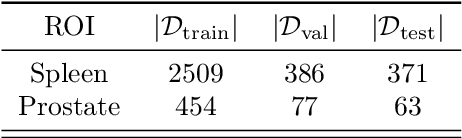
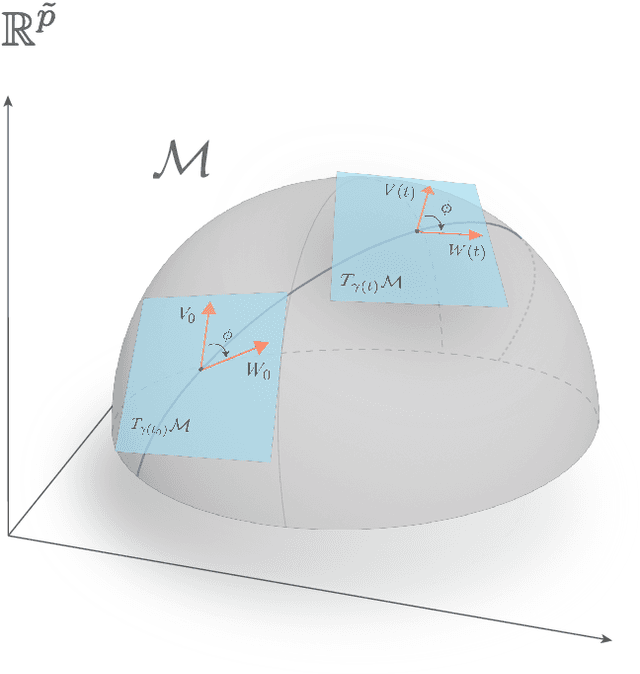
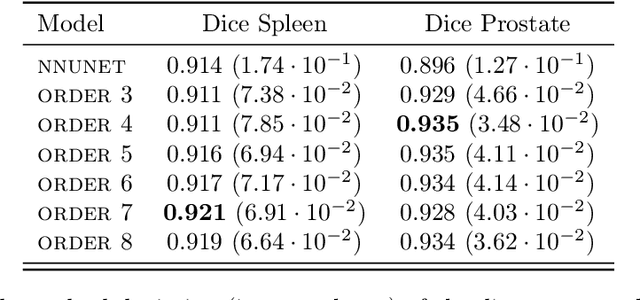
Deep Neural Networks (DNNs) are widely used for their ability to effectively approximate large classes of functions. This flexibility, however, makes the strict enforcement of constraints on DNNs an open problem. Here we present a framework that, under mild assumptions, allows the exact enforcement of constraints on parameterized sets of functions such as DNNs. Instead of imposing "soft'' constraints via additional terms in the loss, we restrict (a subset of) the DNN parameters to a submanifold on which the constraints are satisfied exactly throughout the entire training procedure. We focus on constraints that are outside the scope of equivariant networks used in Geometric Deep Learning. As a major example of the framework, we restrict filters of a Convolutional Neural Network (CNN) to be wavelets, and apply these wavelet networks to the task of contour prediction in the medical domain.

Subpixel object segmentation using wavelets and multi resolution analysis

We propose a novel deep learning framework for fast prediction of boundaries of two-dimensional simply connected domains using wavelets and Multi Resolution Analysis (MRA). The boundaries are modelled as (piecewise) smooth closed curves using wavelets and the so-called Pyramid Algorithm. Our network architecture is a hybrid analog of the U-Net, where the down-sampling path is a two-dimensional encoder with learnable filters, and the upsampling path is a one-dimensional decoder, which builds curves up from low to high resolution levels. Any wavelet basis induced by a MRA can be used. This flexibility allows for incorporation of priors on the smoothness of curves. The effectiveness of the proposed method is demonstrated by delineating boundaries of simply connected domains (organs) in medical images using Debauches wavelets and comparing performance with a U-Net baseline. Our model demonstrates up to 5x faster inference speed compared to the U-Net, while maintaining similar performance in terms of Dice score and Hausdorff distance.