Ravi Shroff
Causal Conceptions of Fairness and their Consequences
Jul 12, 2022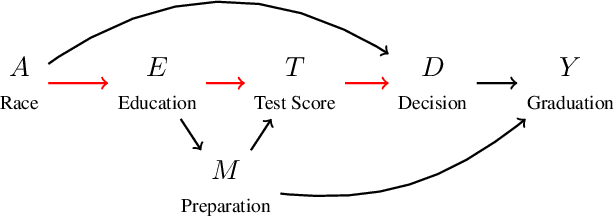
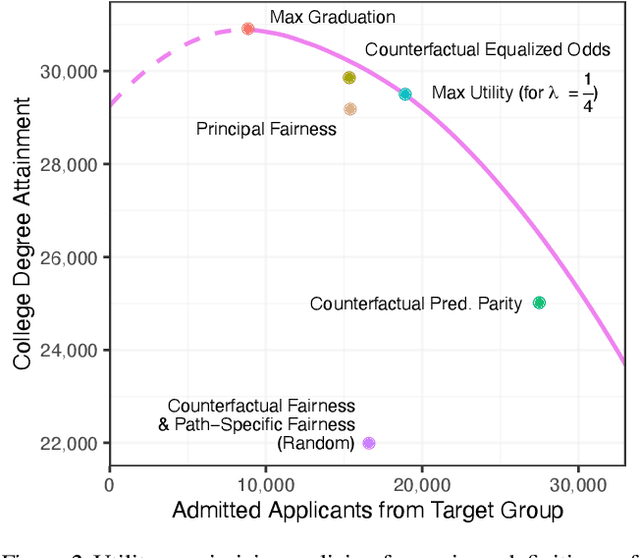
Abstract:Recent work highlights the role of causality in designing equitable decision-making algorithms. It is not immediately clear, however, how existing causal conceptions of fairness relate to one another, or what the consequences are of using these definitions as design principles. Here, we first assemble and categorize popular causal definitions of algorithmic fairness into two broad families: (1) those that constrain the effects of decisions on counterfactual disparities; and (2) those that constrain the effects of legally protected characteristics, like race and gender, on decisions. We then show, analytically and empirically, that both families of definitions \emph{almost always} -- in a measure theoretic sense -- result in strongly Pareto dominated decision policies, meaning there is an alternative, unconstrained policy favored by every stakeholder with preferences drawn from a large, natural class. For example, in the case of college admissions decisions, policies constrained to satisfy causal fairness definitions would be disfavored by every stakeholder with neutral or positive preferences for both academic preparedness and diversity. Indeed, under a prominent definition of causal fairness, we prove the resulting policies require admitting all students with the same probability, regardless of academic qualifications or group membership. Our results highlight formal limitations and potential adverse consequences of common mathematical notions of causal fairness.
* ICML 2022
Simple rules for complex decisions
Apr 02, 2017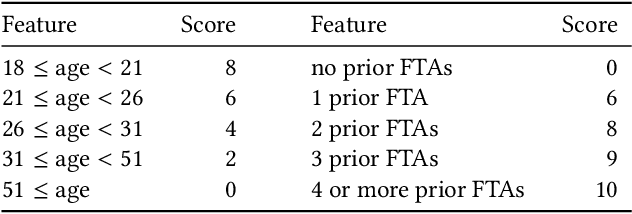
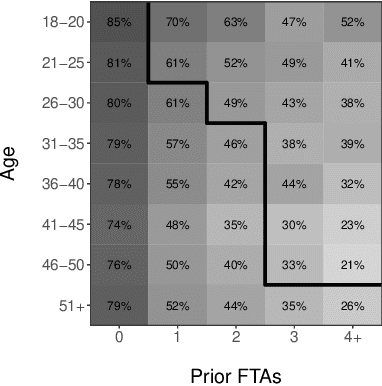
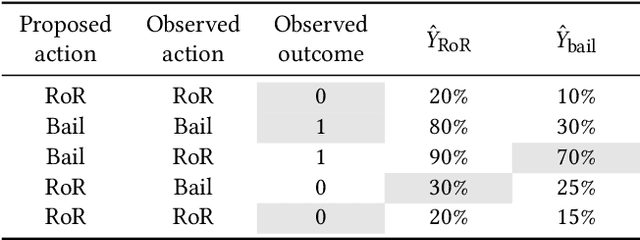
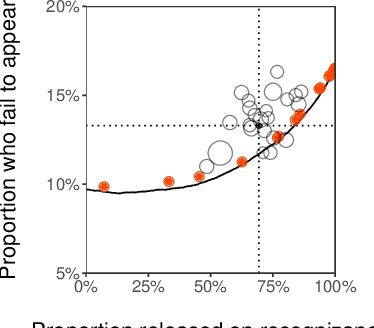
Abstract:From doctors diagnosing patients to judges setting bail, experts often base their decisions on experience and intuition rather than on statistical models. While understandable, relying on intuition over models has often been found to result in inferior outcomes. Here we present a new method, select-regress-and-round, for constructing simple rules that perform well for complex decisions. These rules take the form of a weighted checklist, can be applied mentally, and nonetheless rival the performance of modern machine learning algorithms. Our method for creating these rules is itself simple, and can be carried out by practitioners with basic statistics knowledge. We demonstrate this technique with a detailed case study of judicial decisions to release or detain defendants while they await trial. In this application, as in many policy settings, the effects of proposed decision rules cannot be directly observed from historical data: if a rule recommends releasing a defendant that the judge in reality detained, we do not observe what would have happened under the proposed action. We address this key counterfactual estimation problem by drawing on tools from causal inference. We find that simple rules significantly outperform judges and are on par with decisions derived from random forests trained on all available features. Generalizing to 22 varied decision-making domains, we find this basic result replicates. We conclude with an analytical framework that helps explain why these simple decision rules perform as well as they do.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge