Causal Conceptions of Fairness and their Consequences
Paper and Code
Jul 12, 2022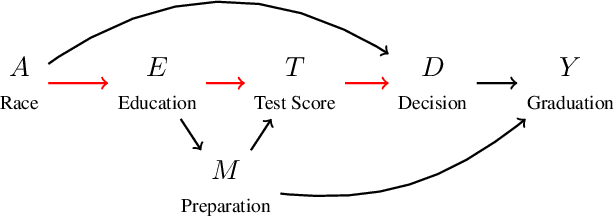
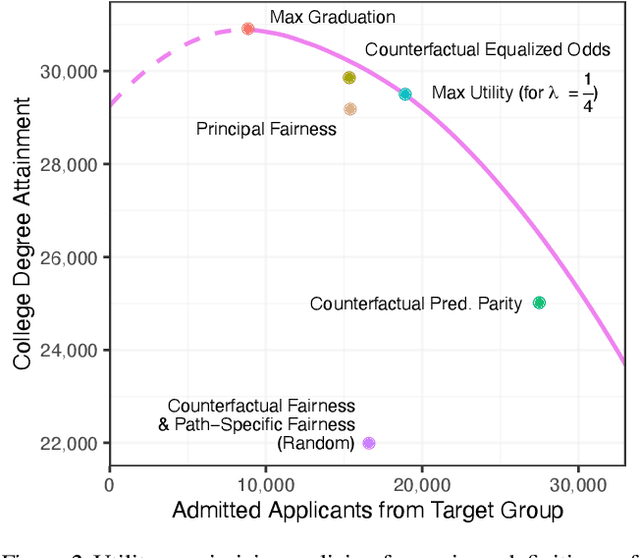
Recent work highlights the role of causality in designing equitable decision-making algorithms. It is not immediately clear, however, how existing causal conceptions of fairness relate to one another, or what the consequences are of using these definitions as design principles. Here, we first assemble and categorize popular causal definitions of algorithmic fairness into two broad families: (1) those that constrain the effects of decisions on counterfactual disparities; and (2) those that constrain the effects of legally protected characteristics, like race and gender, on decisions. We then show, analytically and empirically, that both families of definitions \emph{almost always} -- in a measure theoretic sense -- result in strongly Pareto dominated decision policies, meaning there is an alternative, unconstrained policy favored by every stakeholder with preferences drawn from a large, natural class. For example, in the case of college admissions decisions, policies constrained to satisfy causal fairness definitions would be disfavored by every stakeholder with neutral or positive preferences for both academic preparedness and diversity. Indeed, under a prominent definition of causal fairness, we prove the resulting policies require admitting all students with the same probability, regardless of academic qualifications or group membership. Our results highlight formal limitations and potential adverse consequences of common mathematical notions of causal fairness.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge