Random Fourier Feature Based Deep Learning for Wireless Communications

Deep-learning (DL) has emerged as a powerful machine-learning technique for several classic problems encountered in generic wireless communications. Specifically, random Fourier Features (RFF) based deep-learning has emerged as an attractive solution for several machine-learning problems; yet there is a lacuna of rigorous results to justify the viability of RFF based DL-algorithms in general. To address this gap, we attempt to analytically quantify the viability of RFF based DL. Precisely, in this paper, analytical proofs are presented demonstrating that RFF based DL architectures have lower approximation-error and probability of misclassification as compared to classical DL architectures. In addition, a new distribution-dependent RFF is proposed to facilitate DL architectures with low training-complexity. Through computer simulations, the practical application of the presented analytical results and the proposed distribution-dependent RFF, are depicted for various machine-learning problems encountered in next-generation communication systems such as: a) line of sight (LOS)/non-line of sight (NLOS) classification, and b) message-passing based detection of low-density parity check codes (LDPC) codes over nonlinear visible light communication (VLC) channels. Especially in the low training-data regime, the presented simulations show that significant performance gains are achieved when utilizing RFF maps of observations. Lastly, in all the presented simulations, it is observed that the proposed distribution-dependent RFFs significantly outperform RFFs, which make them useful for potential machine-learning/DL based applications in the context of next-generation communication systems.

Finite Dictionary Variants of the Diffusion KLMS Algorithm

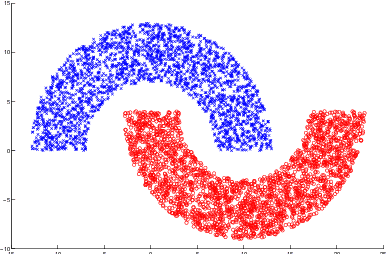
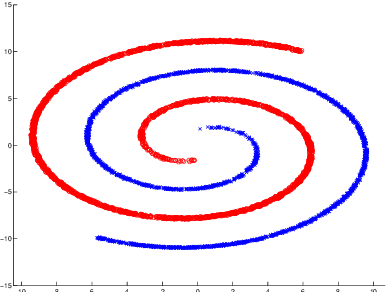
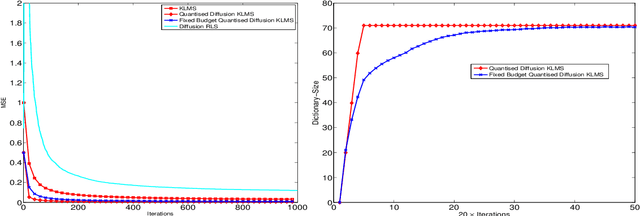
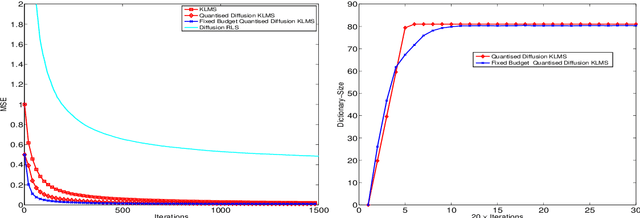
The diffusion based distributed learning approaches have been found to be a viable solution for learning over linearly separable datasets over a network. However, approaches till date are suitable for linearly separable datasets and need to be extended to scenarios in which we need to learn a non-linearity. In such scenarios, the recently proposed diffusion kernel least mean squares (KLMS) has been found to be performing better than diffusion least mean squares (LMS). The drawback of diffusion KLMS is that it requires infinite storage for observations (also called dictionary). This paper formulates the diffusion KLMS in a fixed budget setting such that the storage requirement is curtailed while maintaining appreciable performance in terms of convergence. Simulations have been carried out to validate the two newly proposed algorithms named as quantised diffusion KLMS (QDKLMS) and fixed budget diffusion KLMS (FBDKLMS) against KLMS, which indicate that both the proposed algorithms deliver better performance as compared to the KLMS while reducing the dictionary size storage requirement.

Diffusion-KLMS Algorithm and its Performance Analysis for Non-Linear Distributed Networks

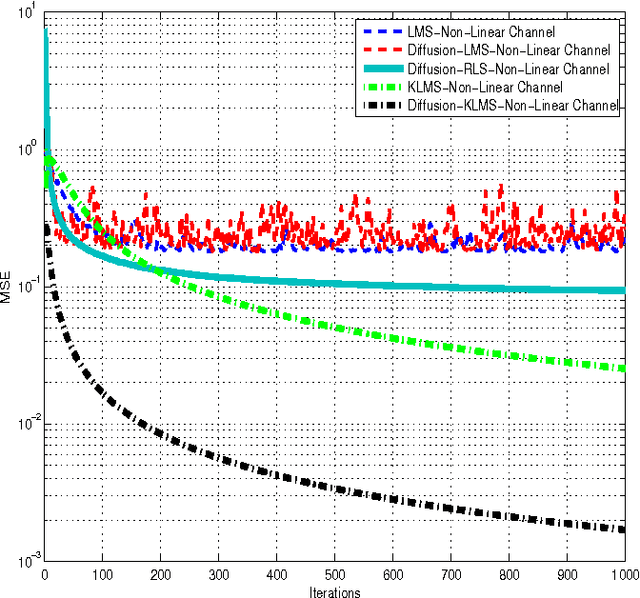
In a distributed network environment, the diffusion-least mean squares (LMS) algorithm gives faster convergence than the original LMS algorithm. It has also been observed that, the diffusion-LMS generally outperforms other distributed LMS algorithms like spatial LMS and incremental LMS. However, both the original LMS and diffusion-LMS are not applicable in non-linear environments where data may not be linearly separable. A variant of LMS called kernel-LMS (KLMS) has been proposed in the literature for such non-linearities. In this paper, we propose kernelised version of diffusion-LMS for non-linear distributed environments. Simulations show that the proposed approach has superior convergence as compared to algorithms of the same genre. We also introduce a technique to predict the transient and steady-state behaviour of the proposed algorithm. The techniques proposed in this work (or algorithms of same genre) can be easily extended to distributed parameter estimation applications like cooperative spectrum sensing and massive multiple input multiple output (MIMO) receiver design which are potential components for 5G communication systems.

A Lower Bound for the Variance of Estimators for Nakagami m Distribution

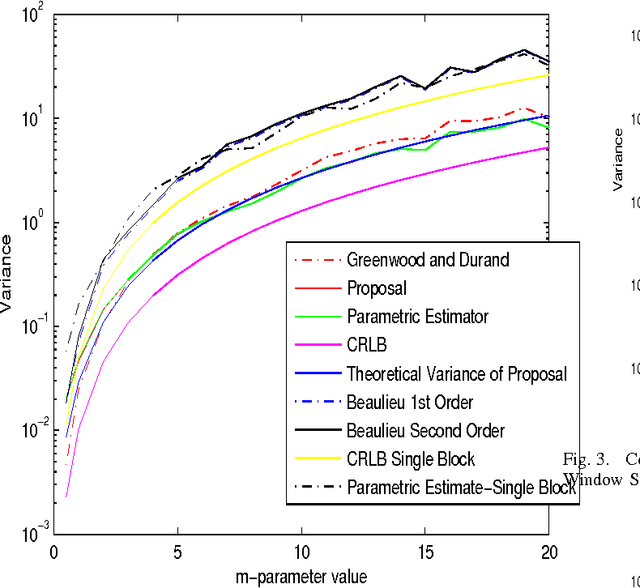
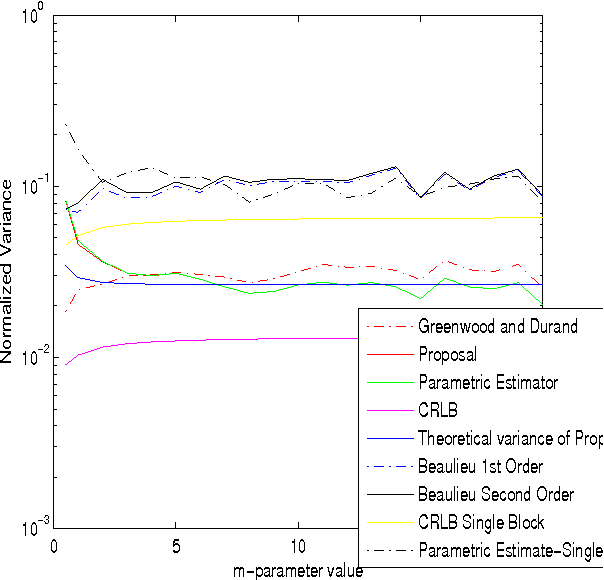
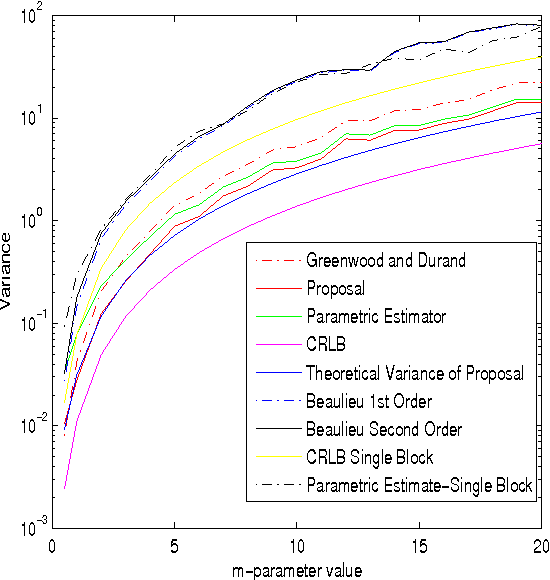
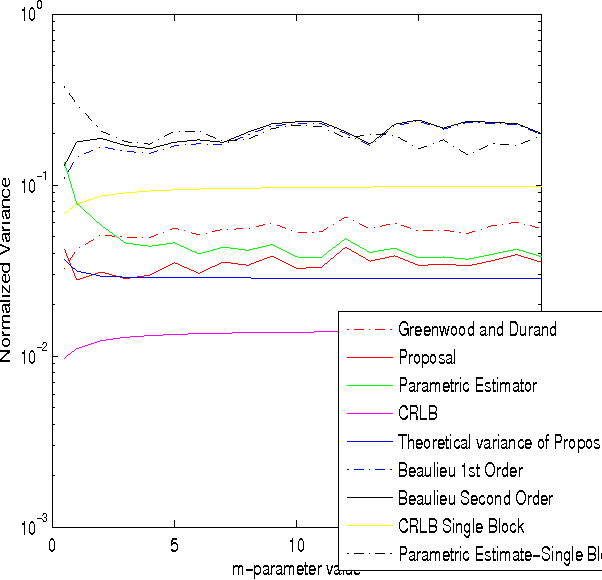
Recently, we have proposed a maximum likelihood iterative algorithm for estimation of the parameters of the Nakagami-m distribution. This technique performs better than state of art estimation techniques for this distribution. This could be of particular use in low data or block based estimation problems. In these scenarios, the estimator should be able to give accurate estimates in the mean square sense with less amounts of data. Also, the estimates should improve with the increase in number of blocks received. In this paper, we see through our simulations, that our proposal is well designed for such requirements. Further, it is well known in the literature that an efficient estimator does not exist for Nakagami-m distribution. In this paper, we derive a theoretical expression for the variance of our proposed estimator. We find that this expression clearly fits the experimental curve for the variance of the proposed estimator. This expression is pretty close to the cramer-rao lower bound(CRLB).

Contraction Principle based Robust Iterative Algorithms for Machine Learning

Iterative algorithms are ubiquitous in the field of data mining. Widely known examples of such algorithms are the least mean square algorithm, backpropagation algorithm of neural networks. Our contribution in this paper is an improvement upon this iterative algorithms in terms of their respective performance metrics and robustness. This improvement is achieved by a new scaling factor which is multiplied to the error term. Our analysis shows that in essence, we are minimizing the corresponding LASSO cost function, which is the reason of its increased robustness. We also give closed form expressions for the number of iterations for convergence and the MSE floor of the original cost function for a minimum targeted value of the L1 norm. As a concluding theme based on the stochastic subgradient algorithm, we give a comparison between the well known Dantzig selector and our algorithm based on contraction principle. By these simulations we attempt to show the optimality of our approach for any widely used parent iterative optimization problem.