Diffusion-KLMS Algorithm and its Performance Analysis for Non-Linear Distributed Networks
Paper and Code
Sep 04, 2015
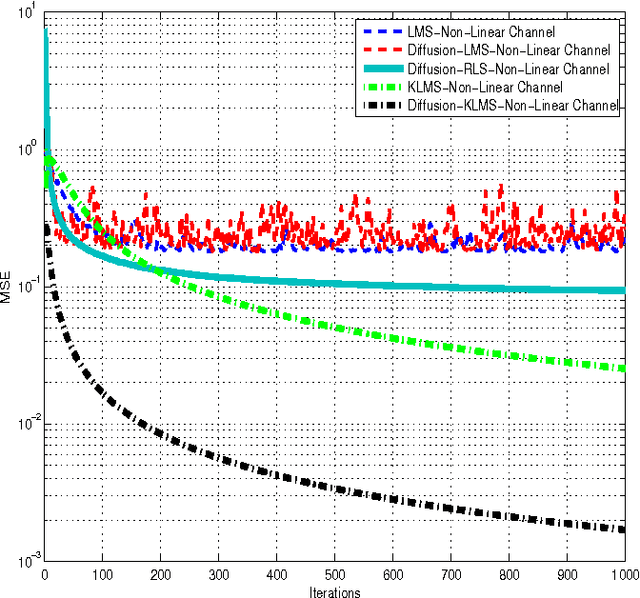


In a distributed network environment, the diffusion-least mean squares (LMS) algorithm gives faster convergence than the original LMS algorithm. It has also been observed that, the diffusion-LMS generally outperforms other distributed LMS algorithms like spatial LMS and incremental LMS. However, both the original LMS and diffusion-LMS are not applicable in non-linear environments where data may not be linearly separable. A variant of LMS called kernel-LMS (KLMS) has been proposed in the literature for such non-linearities. In this paper, we propose kernelised version of diffusion-LMS for non-linear distributed environments. Simulations show that the proposed approach has superior convergence as compared to algorithms of the same genre. We also introduce a technique to predict the transient and steady-state behaviour of the proposed algorithm. The techniques proposed in this work (or algorithms of same genre) can be easily extended to distributed parameter estimation applications like cooperative spectrum sensing and massive multiple input multiple output (MIMO) receiver design which are potential components for 5G communication systems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge