A Lower Bound for the Variance of Estimators for Nakagami m Distribution

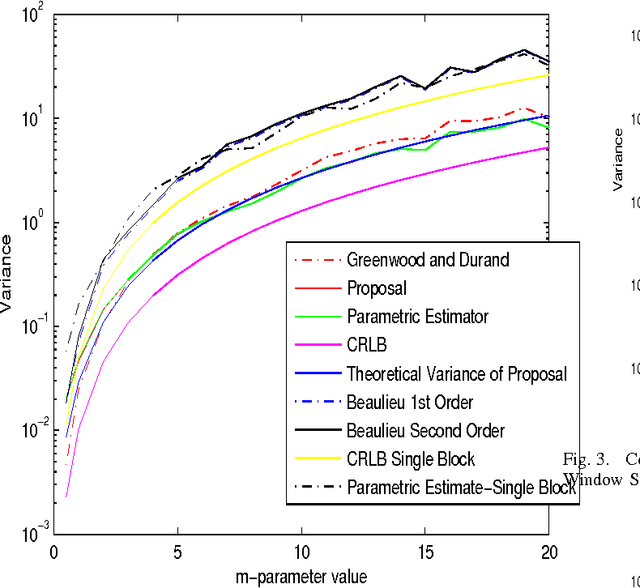
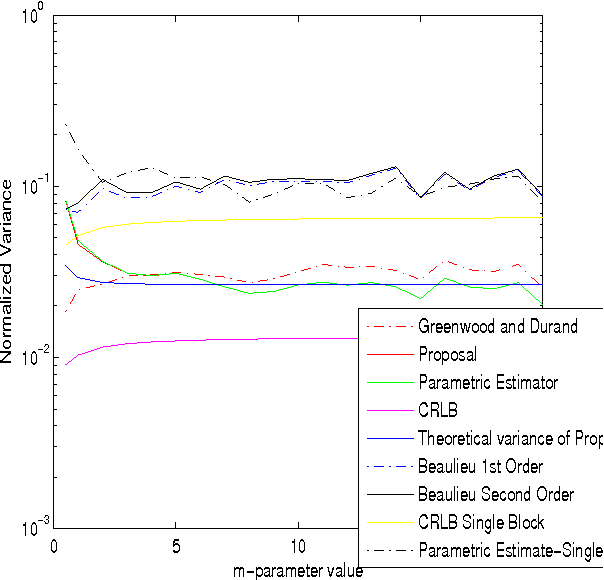
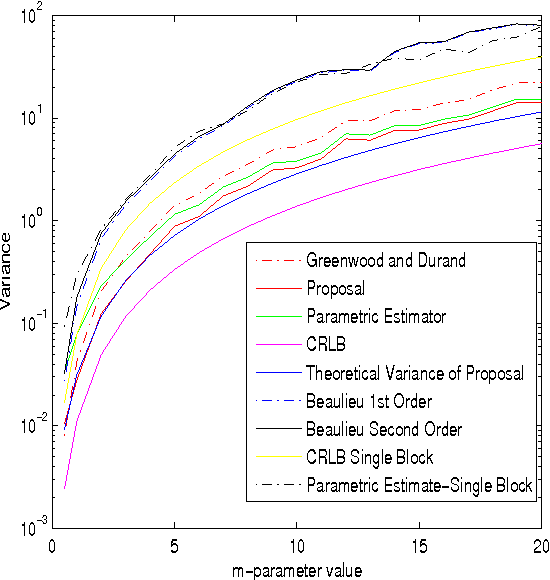
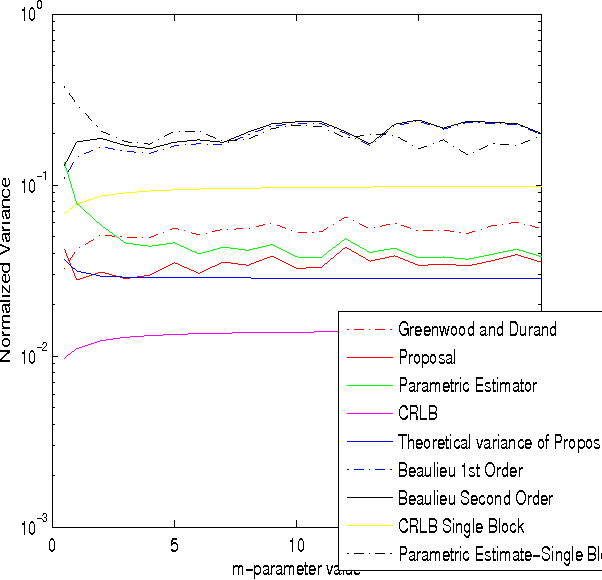
Recently, we have proposed a maximum likelihood iterative algorithm for estimation of the parameters of the Nakagami-m distribution. This technique performs better than state of art estimation techniques for this distribution. This could be of particular use in low data or block based estimation problems. In these scenarios, the estimator should be able to give accurate estimates in the mean square sense with less amounts of data. Also, the estimates should improve with the increase in number of blocks received. In this paper, we see through our simulations, that our proposal is well designed for such requirements. Further, it is well known in the literature that an efficient estimator does not exist for Nakagami-m distribution. In this paper, we derive a theoretical expression for the variance of our proposed estimator. We find that this expression clearly fits the experimental curve for the variance of the proposed estimator. This expression is pretty close to the cramer-rao lower bound(CRLB).