Safe, Aggressive Quadrotor Flight via Reachability-based Trajectory Design

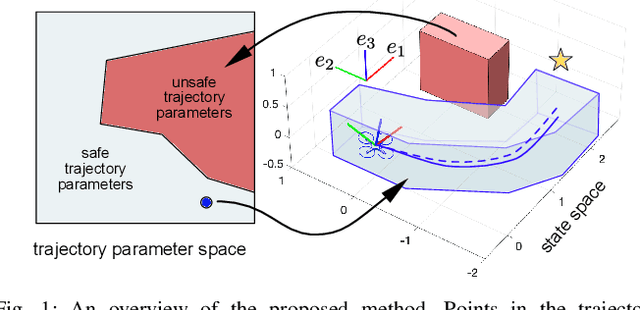
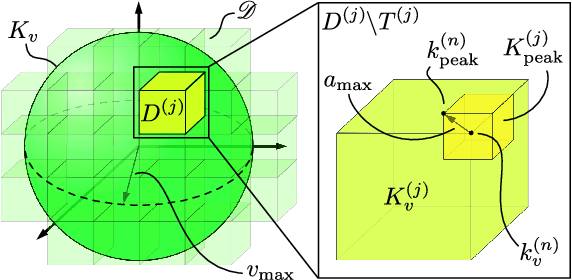
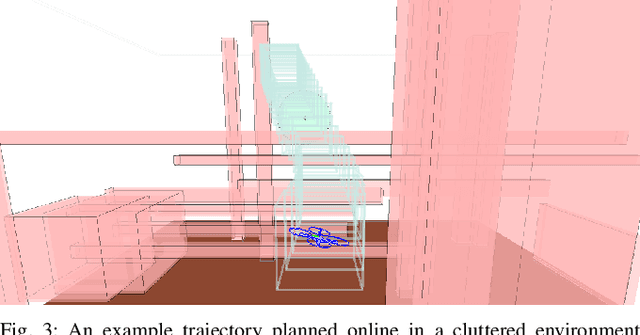
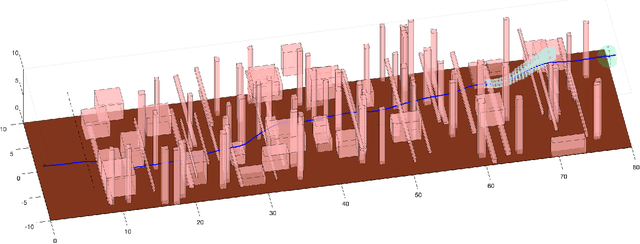
Quadrotors can provide services such as infrastructure inspection and search-and-rescue, which require operating autonomously in cluttered environments. Autonomy is typically achieved with receding-horizon planning, where a short plan is executed while a new one is computed, because sensors receive limited information at any time. To ensure safety and prevent robot loss, plans must be verified as collision free despite uncertainty (e.g, tracking error). Existing spline-based planners dilate obstacles uniformly to compensate for uncertainty, which can be conservative. On the other hand, reachability-based planners can include trajectory-dependent uncertainty as a function of the planned trajectory. This work applies Reachability-based Trajectory Design (RTD) to plan quadrotor trajectories that are safe despite trajectory-dependent tracking error. This is achieved by using zonotopes in a novel way for online planning. Simulations show aggressive flight up to 5 m/s with zero crashes in 500 cluttered, randomized environments.

Safe Trajectory Synthesis for Autonomous Driving in Unforeseen Environments

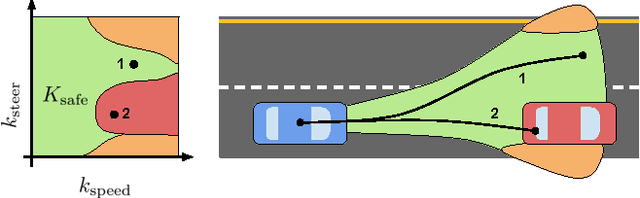
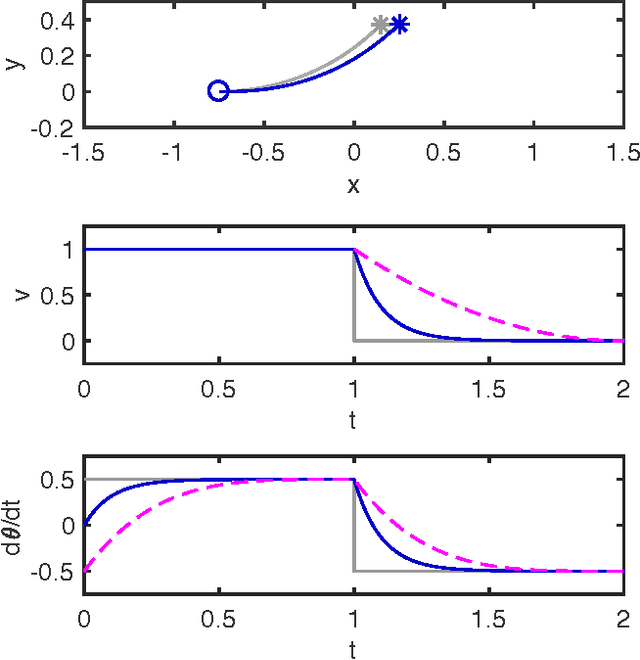
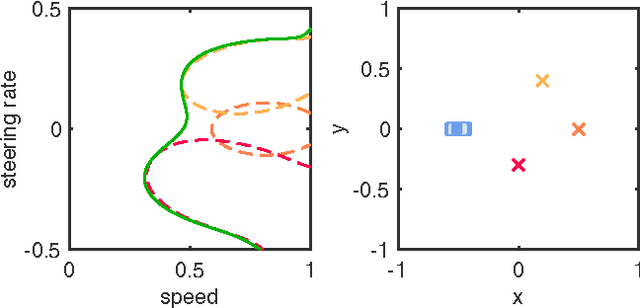
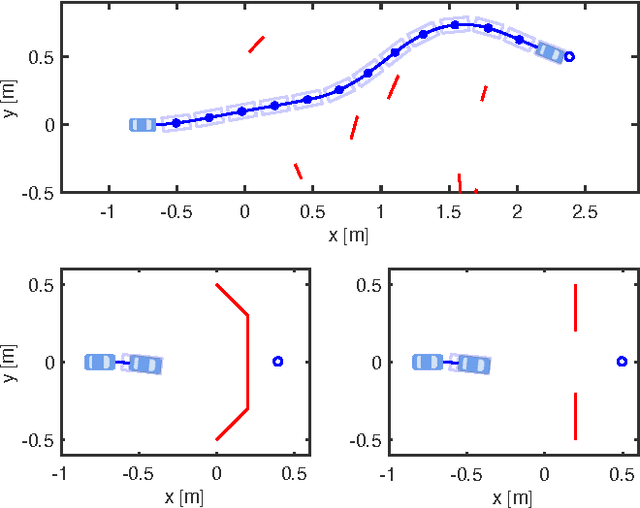
Path planning for autonomous vehicles in arbitrary environments requires a guarantee of safety, but this can be impractical to ensure in real-time when the vehicle is described with a high-fidelity model. To address this problem, this paper develops a method to perform trajectory design by considering a low-fidelity model that accounts for model mismatch. The presented method begins by computing a conservative Forward Reachable Set (FRS) of a high-fidelity model's trajectories produced when tracking trajectories of a low-fidelity model over a finite time horizon. At runtime, the vehicle intersects this FRS with obstacles in the environment to eliminate trajectories that can lead to a collision, then selects an optimal plan from the remaining safe set. By bounding the time for this set intersection and subsequent path selection, this paper proves a lower bound for the FRS time horizon and sensing horizon to guarantee safety. This method is demonstrated in simulation using a kinematic Dubin's car as the low-fidelity model and a dynamic unicycle as the high-fidelity model.