On Graphical Modeling of Preference and Importance

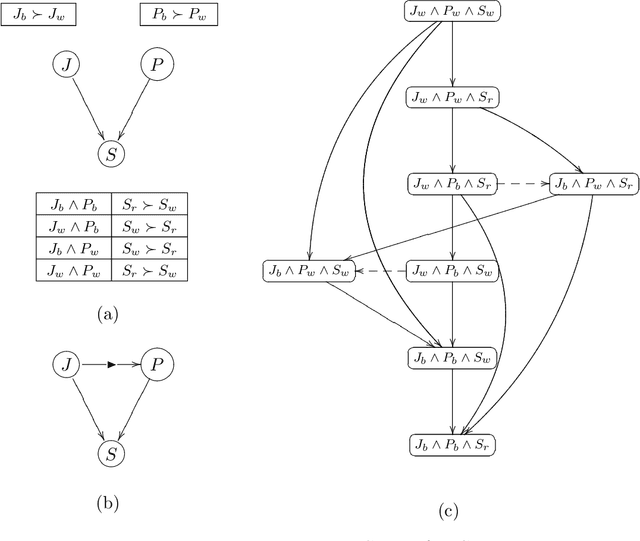
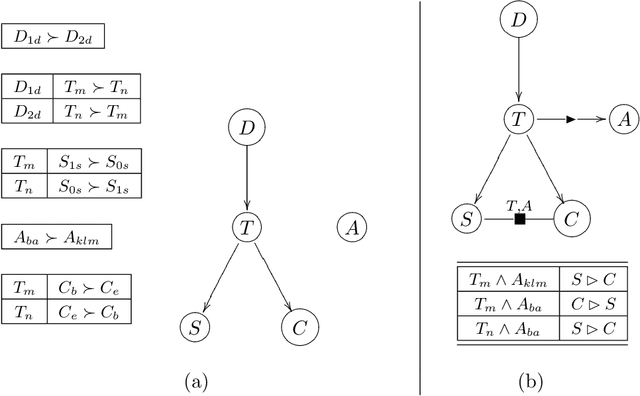
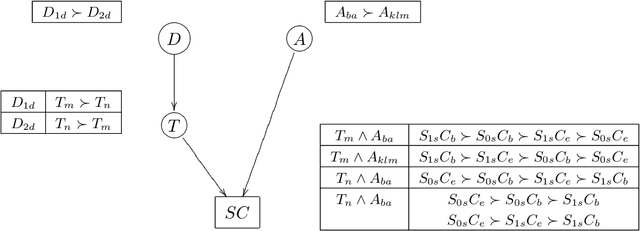
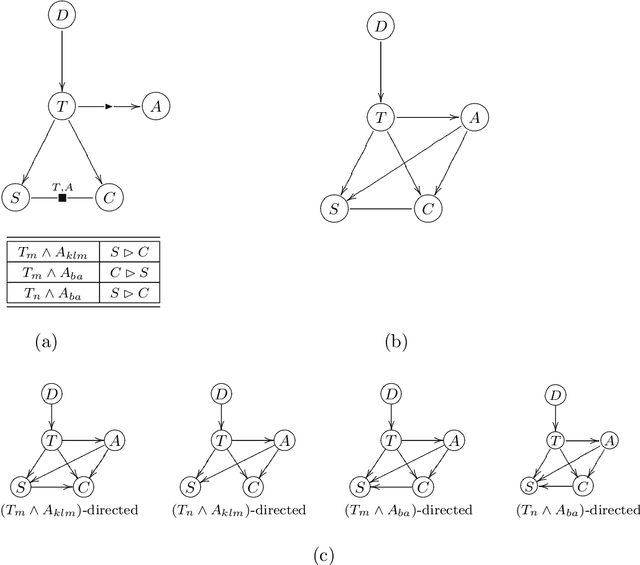
In recent years, CP-nets have emerged as a useful tool for supporting preference elicitation, reasoning, and representation. CP-nets capture and support reasoning with qualitative conditional preference statements, statements that are relatively natural for users to express. In this paper, we extend the CP-nets formalism to handle another class of very natural qualitative statements one often uses in expressing preferences in daily life - statements of relative importance of attributes. The resulting formalism, TCP-nets, maintains the spirit of CP-nets, in that it remains focused on using only simple and natural preference statements, uses the ceteris paribus semantics, and utilizes a graphical representation of this information to reason about its consistency and to perform, possibly constrained, optimization using it. The extra expressiveness it provides allows us to better model tradeoffs users would like to make, more faithfully representing their preferences.

CP-nets: A Tool for Representing and Reasoning withConditional Ceteris Paribus Preference Statements

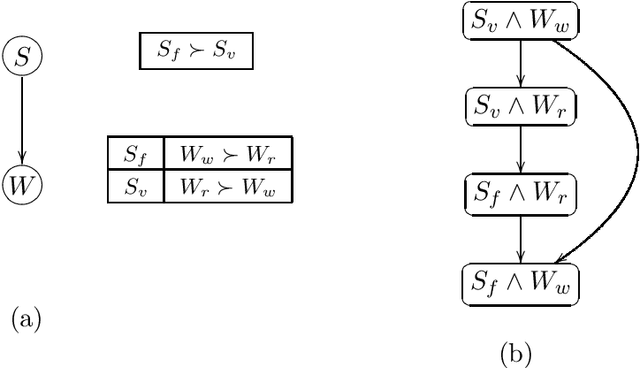
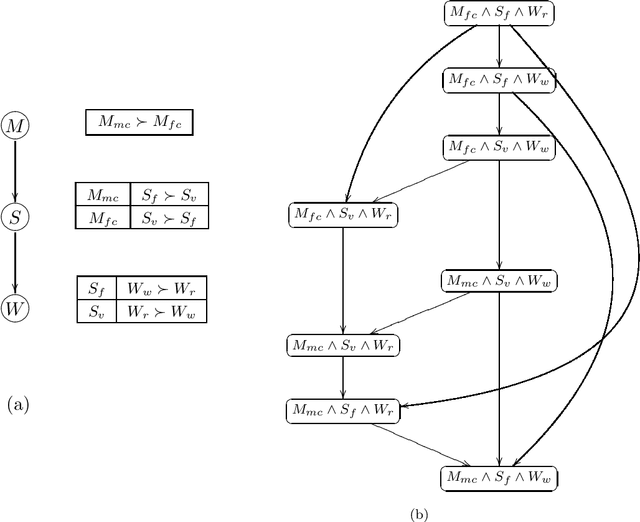
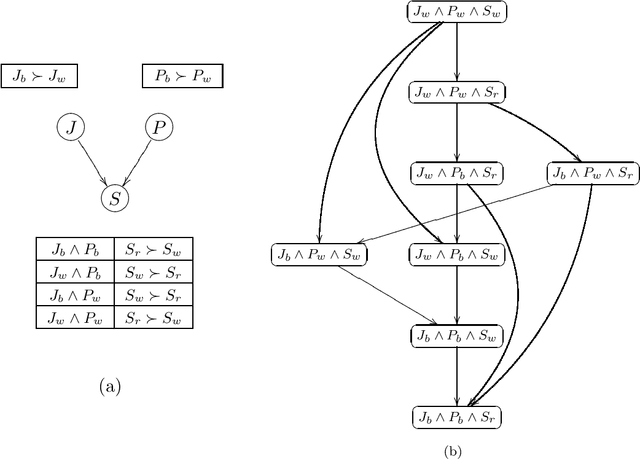
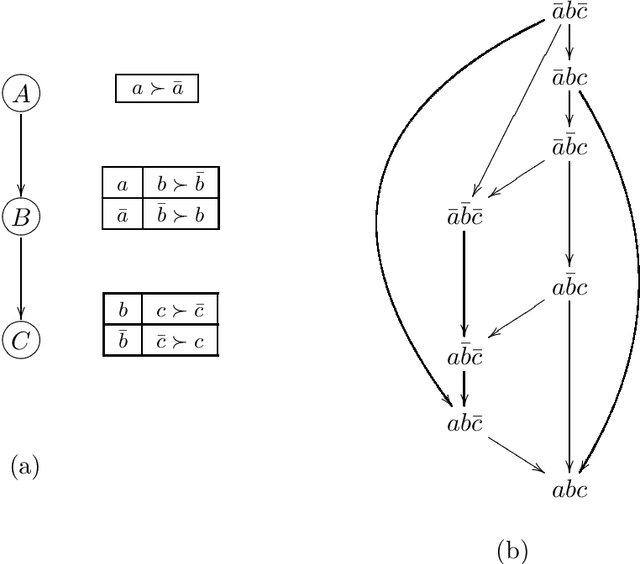
Information about user preferences plays a key role in automated decision making. In many domains it is desirable to assess such preferences in a qualitative rather than quantitative way. In this paper, we propose a qualitative graphical representation of preferences that reflects conditional dependence and independence of preference statements under a ceteris paribus (all else being equal) interpretation. Such a representation is often compact and arguably quite natural in many circumstances. We provide a formal semantics for this model, and describe how the structure of the network can be exploited in several inference tasks, such as determining whether one outcome dominates (is preferred to) another, ordering a set outcomes according to the preference relation, and constructing the best outcome subject to available evidence.

Learning to Coordinate Efficiently: A Model-based Approach

In common-interest stochastic games all players receive an identical payoff. Players participating in such games must learn to coordinate with each other in order to receive the highest-possible value. A number of reinforcement learning algorithms have been proposed for this problem, and some have been shown to converge to good solutions in the limit. In this paper we show that using very simple model-based algorithms, much better (i.e., polynomial) convergence rates can be attained. Moreover, our model-based algorithms are guaranteed to converge to the optimal value, unlike many of the existing algorithms.

Structure and Complexity in Planning with Unary Operators

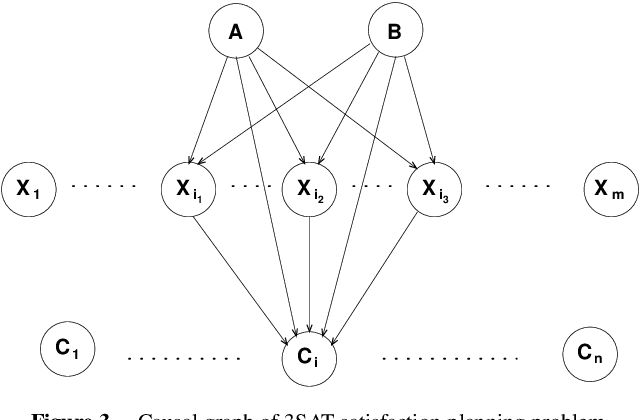
Unary operator domains -- i.e., domains in which operators have a single effect -- arise naturally in many control problems. In its most general form, the problem of STRIPS planning in unary operator domains is known to be as hard as the general STRIPS planning problem -- both are PSPACE-complete. However, unary operator domains induce a natural structure, called the domain's causal graph. This graph relates between the preconditions and effect of each domain operator. Causal graphs were exploited by Williams and Nayak in order to analyze plan generation for one of the controllers in NASA's Deep-Space One spacecraft. There, they utilized the fact that when this graph is acyclic, a serialization ordering over any subgoal can be obtained quickly. In this paper we conduct a comprehensive study of the relationship between the structure of a domain's causal graph and the complexity of planning in this domain. On the positive side, we show that a non-trivial polynomial time plan generation algorithm exists for domains whose causal graph induces a polytree with a constant bound on its node indegree. On the negative side, we show that even plan existence is hard when the graph is a directed-path singly connected DAG. More generally, we show that the number of paths in the causal graph is closely related to the complexity of planning in the associated domain. Finally we relate our results to the question of complexity of planning with serializable subgoals.

Partial-Order Planning with Concurrent Interacting Actions

In order to generate plans for agents with multiple actuators, agent teams, or distributed controllers, we must be able to represent and plan using concurrent actions with interacting effects. This has historically been considered a challenging task requiring a temporal planner with the ability to reason explicitly about time. We show that with simple modifications, the STRIPS action representation language can be used to represent interacting actions. Moreover, algorithms for partial-order planning require only small modifications in order to be applied in such multiagent domains. We demonstrate this fact by developing a sound and complete partial-order planner for planning with concurrent interacting actions, POMP, that extends existing partial-order planners in a straightforward way. These results open the way to the use of partial-order planners for the centralized control of cooperative multiagent systems.

On Partially Controlled Multi-Agent Systems

Motivated by the control theoretic distinction between controllable and uncontrollable events, we distinguish between two types of agents within a multi-agent system: controllable agents, which are directly controlled by the system's designer, and uncontrollable agents, which are not under the designer's direct control. We refer to such systems as partially controlled multi-agent systems, and we investigate how one might influence the behavior of the uncontrolled agents through appropriate design of the controlled agents. In particular, we wish to understand which problems are naturally described in these terms, what methods can be applied to influence the uncontrollable agents, the effectiveness of such methods, and whether similar methods work across different domains. Using a game-theoretic framework, this paper studies the design of partially controlled multi-agent systems in two contexts: in one context, the uncontrollable agents are expected utility maximizers, while in the other they are reinforcement learners. We suggest different techniques for controlling agents' behavior in each domain, assess their success, and examine their relationship.