K-Implementation

This paper discusses an interested party who wishes to influence the behavior of agents in a game (multi-agent interaction), which is not under his control. The interested party cannot design a new game, cannot enforce agents' behavior, cannot enforce payments by the agents, and cannot prohibit strategies available to the agents. However, he can influence the outcome of the game by committing to non-negative monetary transfers for the different strategy profiles that may be selected by the agents. The interested party assumes that agents are rational in the commonly agreed sense that they do not use dominated strategies. Hence, a certain subset of outcomes is implemented in a given game if by adding non-negative payments, rational players will necessarily produce an outcome in this subset. Obviously, by making sufficiently big payments one can implement any desirable outcome. The question is what is the cost of implementation? In this paper we introduce the notion of k-implementation of a desired set of strategy profiles, where k stands for the amount of payment that need to be actually made in order to implement desirable outcomes. A major point in k-implementation is that monetary offers need not necessarily materialize when following desired behaviors. We define and study k-implementation in the contexts of games with complete and incomplete information. In the latter case we mainly focus on the VCG games. Our setting is later extended to deal with mixed strategies using correlation devices. Together, the paper introduces and studies the implementation of desirable outcomes by a reliable party who cannot modify game rules (i.e. provide protocols), complementing previous work in mechanism design, while making it more applicable to many realistic CS settings.

Learning to Coordinate Efficiently: A Model-based Approach

In common-interest stochastic games all players receive an identical payoff. Players participating in such games must learn to coordinate with each other in order to receive the highest-possible value. A number of reinforcement learning algorithms have been proposed for this problem, and some have been shown to converge to good solutions in the limit. In this paper we show that using very simple model-based algorithms, much better (i.e., polynomial) convergence rates can be attained. Moreover, our model-based algorithms are guaranteed to converge to the optimal value, unlike many of the existing algorithms.

Competitive Safety Analysis: Robust Decision-Making in Multi-Agent Systems

Much work in AI deals with the selection of proper actions in a given (known or unknown) environment. However, the way to select a proper action when facing other agents is quite unclear. Most work in AI adopts classical game-theoretic equilibrium analysis to predict agent behavior in such settings. This approach however does not provide us with any guarantee for the agent. In this paper we introduce competitive safety analysis. This approach bridges the gap between the desired normative AI approach, where a strategy should be selected in order to guarantee a desired payoff, and equilibrium analysis. We show that a safety level strategy is able to guarantee the value obtained in a Nash equilibrium, in several classical computer science settings. Then, we discuss the concept of competitive safety strategies, and illustrate its use in a decentralized load balancing setting, typical to network problems. In particular, we show that when we have many agents, it is possible to guarantee an expected payoff which is a factor of 8/9 of the payoff obtained in a Nash equilibrium. Our discussion of competitive safety analysis for decentralized load balancing is further developed to deal with many communication links and arbitrary speeds. Finally, we discuss the extension of the above concepts to Bayesian games, and illustrate their use in a basic auctions setup.

Dynamic Non-Bayesian Decision Making

The model of a non-Bayesian agent who faces a repeated game with incomplete information against Nature is an appropriate tool for modeling general agent-environment interactions. In such a model the environment state (controlled by Nature) may change arbitrarily, and the feedback/reward function is initially unknown. The agent is not Bayesian, that is he does not form a prior probability neither on the state selection strategy of Nature, nor on his reward function. A policy for the agent is a function which assigns an action to every history of observations and actions. Two basic feedback structures are considered. In one of them -- the perfect monitoring case -- the agent is able to observe the previous environment state as part of his feedback, while in the other -- the imperfect monitoring case -- all that is available to the agent is the reward obtained. Both of these settings refer to partially observable processes, where the current environment state is unknown. Our main result refers to the competitive ratio criterion in the perfect monitoring case. We prove the existence of an efficient stochastic policy that ensures that the competitive ratio is obtained at almost all stages with an arbitrarily high probability, where efficiency is measured in terms of rate of convergence. It is further shown that such an optimal policy does not exist in the imperfect monitoring case. Moreover, it is proved that in the perfect monitoring case there does not exist a deterministic policy that satisfies our long run optimality criterion. In addition, we discuss the maxmin criterion and prove that a deterministic efficient optimal strategy does exist in the imperfect monitoring case under this criterion. Finally we show that our approach to long-run optimality can be viewed as qualitative, which distinguishes it from previous work in this area.

On Partially Controlled Multi-Agent Systems

Motivated by the control theoretic distinction between controllable and uncontrollable events, we distinguish between two types of agents within a multi-agent system: controllable agents, which are directly controlled by the system's designer, and uncontrollable agents, which are not under the designer's direct control. We refer to such systems as partially controlled multi-agent systems, and we investigate how one might influence the behavior of the uncontrolled agents through appropriate design of the controlled agents. In particular, we wish to understand which problems are naturally described in these terms, what methods can be applied to influence the uncontrollable agents, the effectiveness of such methods, and whether similar methods work across different domains. Using a game-theoretic framework, this paper studies the design of partially controlled multi-agent systems in two contexts: in one context, the uncontrollable agents are expected utility maximizers, while in the other they are reinforcement learners. We suggest different techniques for controlling agents' behavior in each domain, assess their success, and examine their relationship.

Adaptive Load Balancing: A Study in Multi-Agent Learning

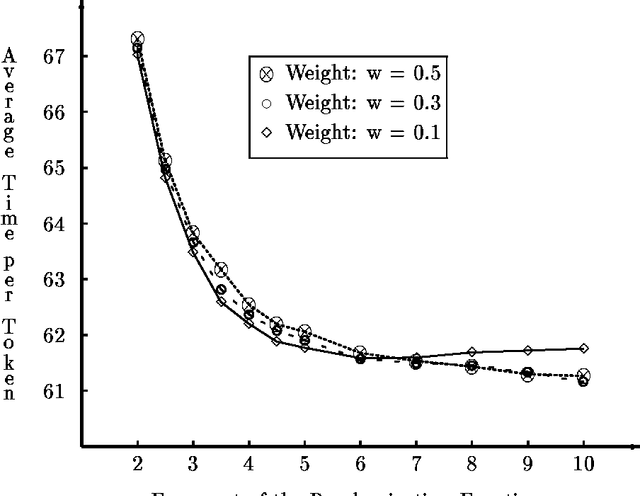
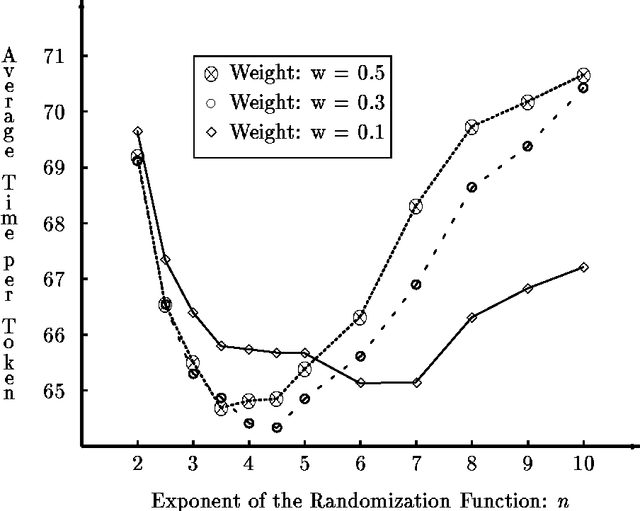
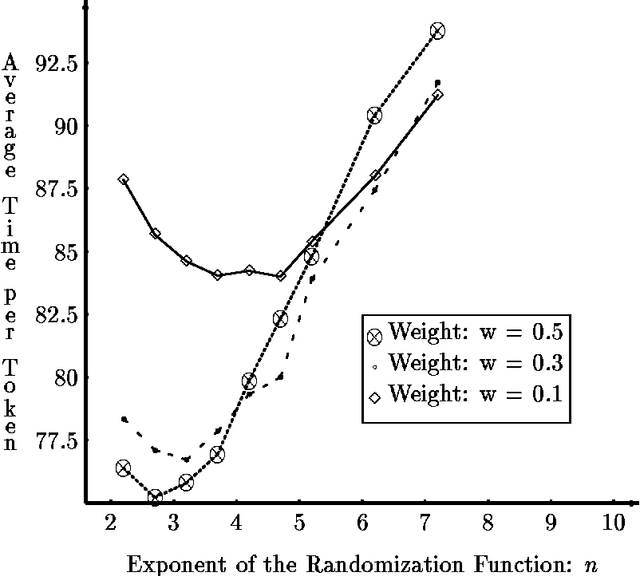
We study the process of multi-agent reinforcement learning in the context of load balancing in a distributed system, without use of either central coordination or explicit communication. We first define a precise framework in which to study adaptive load balancing, important features of which are its stochastic nature and the purely local information available to individual agents. Given this framework, we show illuminating results on the interplay between basic adaptive behavior parameters and their effect on system efficiency. We then investigate the properties of adaptive load balancing in heterogeneous populations, and address the issue of exploration vs. exploitation in that context. Finally, we show that naive use of communication may not improve, and might even harm system efficiency.

On Planning while Learning

This paper introduces a framework for Planning while Learning where an agent is given a goal to achieve in an environment whose behavior is only partially known to the agent. We discuss the tractability of various plan-design processes. We show that for a large natural class of Planning while Learning systems, a plan can be presented and verified in a reasonable time. However, coming up algorithmically with a plan, even for simple classes of systems is apparently intractable. We emphasize the role of off-line plan-design processes, and show that, in most natural cases, the verification (projection) part can be carried out in an efficient algorithmic manner.